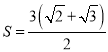题目内容
【题目】已知向量 ![]() 与
与 ![]() 互相垂直,其中
互相垂直,其中 ![]() .
.
(1)求sinθ和cosθ的值;
(2)若 ![]() ,
, ![]() 求cosφ的值.
求cosφ的值.
【答案】
(1)解:∵ ![]() 与
与 ![]() 互相垂直,则
互相垂直,则 ![]() ,
,
即sinθ=2cosθ,代入sin2θ+cos2θ=1得 ![]() ,又
,又 ![]() ,
,
∴ ![]()
(2)解:0<φ< ![]() ,
, ![]() ,
,
∴﹣ ![]() <θ﹣φ<
<θ﹣φ< ![]() ,则cos(θ﹣φ)=
,则cos(θ﹣φ)= ![]() =
= ![]() ,
,
∴cosφ=cos[θ﹣(θ﹣φ)]=cosθcos(θ﹣φ)+sinθsin(θ﹣φ)= ![]()
【解析】(1)根据两向量垂直,求得sinθ和cosθ的关系代入sin2θ+cos2θ=1中求得sinθ和cosθ的值.(2)先利用φ和θ的范围确定θ﹣φ的范围,进而利用同角三角函数基本关系求得cos(θ﹣φ)的值,进而利用cosφ=cos[θ﹣(θ﹣)]根据两角和公式求得答案.
【考点精析】本题主要考查了同角三角函数基本关系的运用的相关知识点,需要掌握同角三角函数的基本关系:![]()
![]() ;
;![]()
![]() ;(3) 倒数关系:
;(3) 倒数关系:![]() 才能正确解答此题.
才能正确解答此题.

练习册系列答案
相关题目
【题目】公车私用、超编配车等现象一直饱受诟病,省机关事务管理局认真贯彻落实党中央、国务院有关公务用车配备使用管理办法,积极推进公务用车制度改革.某机关单位有车牌尾号为2的汽车A和尾号为6的汽车B,两车分属于两个独立业务部门.为配合用车制度对一段时间内两辆汽车的用车记录进行统计,在非限行日,A车日出车频率0.6,B车日出车频率0.5,该地区汽车限行规定如下:
车尾号 | 0和5 | 1和6 | 2和7 | 3和8 | 4和9 |
限行日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
现将汽车日出车频率理解为日出车概率,且A,B两车出车情况相互独立.
(1)求该单位在星期一恰好出车一台的概率;
(2)设X表示该单位在星期一与星期二两天的出车台数之和,求X的分布列及其数学期望E(X).