题目内容
9．已知正四棱台上底面边长为4cm，下底面边长为10cm，侧棱为5cm，求它的斜高和体积．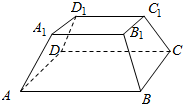
分析 如图：在正四棱台ABCD-A1B1C1D1中，找出高和斜高，分别用勾股定理求出斜高和高．然后求解体积．
解答 
解：如图：正四棱台ABCD-A1B1C1D1 中，高h=A1O，斜高 h′=A1E，OE=$\frac{10-4}{2}$=3cm．AE=OE=3cm，侧棱AA1=5cm，A1E=$\sqrt{{{AA}_{1}}^{2}-{AE}^{2}}$=4cm．A1O=$\sqrt{{{AA}_{1}}^{2}-{OE}^{2}}$=$\sqrt{7}$cm．
棱台的体积：V=$\frac{1}{3}×\sqrt{7}×（16+100+\sqrt{1600}）$=$\frac{156\sqrt{7}}{3}$=52$\sqrt{7}$（cm3）．
正四棱台的斜高：4cm；体积为：52$\sqrt{7}$cm3．
点评 本题考查正四棱台的性质，构造直角梯形和直角三角形，利用勾股定理是解决问题的关键．
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
如图，三棱柱ABC-A1B1C1中，侧棱AA1⊥平面ABC，△ABC为等腰直角三角形，∠BAC=90°，且AB=AA1=2，E，F分别是CC1，BC的中点．
4．在椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）上取三点，其横坐标满足x1+x3=2x2，三点与某一焦点的连线段长分别为r1，r2，r3．则r1，r2，r3满足（ ）
| A． | r1，r2，r3成等差数列 | B． | $\frac{1}{{r}_{1}}$+$\frac{1}{{r}_{2}}$=$\frac{2}{{r}_{3}}$ | ||
| C． | r1，r2，r3成等比数列 | D． | 以上结论全不对 |