题目内容
【题目】已知定点M(﹣ ![]() ),N是圆C:(x﹣
),N是圆C:(x﹣ ![]() )2+y2=16(C为圆心) 上的动点,MN的垂直平分线与NC交于点E.
)2+y2=16(C为圆心) 上的动点,MN的垂直平分线与NC交于点E.
(1)求动点E的轨迹方程C1;
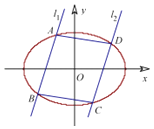
(2)直线l与轨迹C1交于P,Q两点,与抛物线C2:x2=4y交于A,B两点,且抛物线C2在点A,B处的切线垂直相交于S,设点S到直线l的距离为d,试问:是否存在直线l,使得d= ![]() ?若存在,求直线l的方程;若不存在,请说明理由.
?若存在,求直线l的方程;若不存在,请说明理由.
【答案】
(1)解:依题意有:|EM|+|EC|=|EN|+|EC|=|NC|=4,故动点E的轨迹为以M,C为焦点,长轴为4的椭圆.
于是: ![]() ,从而
,从而 ![]() ,故动点E的轨迹方程C1为:
,故动点E的轨迹方程C1为: ![]()
(2)解:设直线l:y=kx+m,A(x1,y1),B(x2,y2),P(x3,y3)Q(x4,y4),由 ![]() ,
,
得:x2﹣4kx﹣4m=0,故x1+x2=4k,x1x2=﹣4m.
由x2=4y得: ![]() ,即切线斜率
,即切线斜率 ![]() .
.
于是: ![]() ,
,
由PA⊥PB得; ![]() ,
,
解得:m=1,
这说明直线l过抛物线C2的焦点F,由 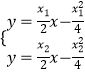 ,
,
得: ![]() 即S(2k,﹣1).
即S(2k,﹣1).
于是:点S(2k,﹣1)到直线l:kx﹣y+1=0的距离 ![]() ,
,
由 ![]() 得:(1+2k2)x2+4kx﹣2=0,
得:(1+2k2)x2+4kx﹣2=0,
从而 ![]() ,
,
同理:|AB|=4(1+k2),
由 ![]() 得
得 ![]() ,
,
化简整理,得:28k4+36k2+7=0,此方程无解,
所以不存在直线l,使得 ![]()
【解析】(1)由题意可知::|EM|+|EC|=|EN|+|EC|=|NC|=4,故动点E的轨迹为以M,C为焦点,长轴为4的椭圆,分别求得a、b和c的值,求得动点E的轨迹方程C1;(2)设出直线l的方程,代入椭圆方程,由韦达定理求得x1+x2及x1x2 , 利用导数法求得直线PA和PB的斜率,由PA⊥PB,求得m的值,直线l过抛物线C2的焦点F,求得交点S的坐标,根据点到直线的距离公式,求得S到到直线l:kx﹣y+1=0的距离d,根据弦长公式求得丨PQ丨及|AB|,由 ![]() ,求得28k4+36k2+7=0,此方程无解,不存在直线l,使得
,求得28k4+36k2+7=0,此方程无解,不存在直线l,使得 ![]() .
.

 寒假学与练系列答案
寒假学与练系列答案