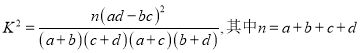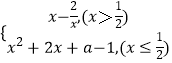题目内容
【题目】已知函数f(x)=log2(x+1),g(x)=log2(3x+1).
(1)求出使g(x)≥f(x)成立的x的取值范围;
(2)当x∈[0,+∞)时,求函数y=g(x)﹣f(x)的值域.
【答案】
(1)
解:∵f(x)=log2(x+1),g(x)=log2(3x+1),g(x)≥f(x),
∴3x+1≥x+1>0,
∴x≥0.
即使g(x)≥f(x)成立的x的取值范围为[0,+∞)
(2)
解:∵y=g(x)﹣f(x)
=log2(3x+1)﹣log2(x+1)
=log2 ![]() (x≥0).
(x≥0).
令h(x)= ![]() =3﹣
=3﹣ ![]() ,
,
则h(x)为[0,+∞)上的增函数,
∴1≤h(x)<3,
故y=g(x)﹣f(x)∈[0,log23],
即函数y=g(x)﹣f(x)的值域为[0,log23]
【解析】(1)利用对数函数y=log2x的单调性即可求得g(x)≥f(x)成立的x的取值范围;(2)分析函数y=g(x)﹣f(x)的单调性,结合x∈[0,+∞)可得函数y=g(x)﹣f(x)的值域.
【考点精析】利用对数函数的定义域和对数函数的单调区间对题目进行判断即可得到答案,需要熟知对数函数的定义域范围:(0,+∞);a变化对图象的影响:在第一象限内,a越大图象越靠低;在第四象限内,a越大图象越靠高.

 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案【题目】电视传媒公司为了解某地区电视观众对里约奥运会的收视情况,随机抽取了100名观众进行调查,其中女性有55名,下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:
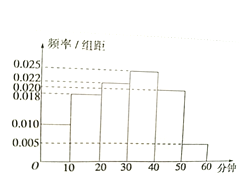
将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”。已知“体育迷”中有10名女性。
(1)试求“体育迷”中的男性观众人数;
(2)据此资料完成![]() 列联表,你是否认为“体育迷”与性别有关?
列联表,你是否认为“体育迷”与性别有关?
非体育迷 | 体育迷 | 合计 | |
男 | |||
女 | |||
合计 |
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
临界值表供参考参考公式: