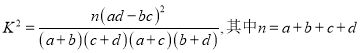题目内容
【题目】已知f(x),g(x)都是定义在R上的函数,并满足:
1)f(x)=2axg(x),(a>0,a≠1);
2)g(x)≠0;
3)f(x)g′(x)<f′(x)g(x)且 ![]() +
+ ![]() =5,则a= .
=5,则a= .
【答案】2
【解析】解:由(1)、(2)得, ![]() ,
,
因为 ![]() +
+ ![]() =5,所以2a+2a﹣1=5,解得a=
=5,所以2a+2a﹣1=5,解得a= ![]() 或a=2,
或a=2,
由f(x)g′(x)<f′(x)g(x),得 ![]() >0,
>0,
所以 ![]() 单调递增,故a>1,
单调递增,故a>1,
所以a=2,
所以答案是:2.
【考点精析】掌握基本求导法则和函数的零点是解答本题的根本,需要知道若两个函数可导,则它们和、差、积、商必可导;若两个函数均不可导,则它们的和、差、积、商不一定不可导;函数的零点就是方程的实数根,亦即函数的图象与轴交点的横坐标.即:方程有实数根,函数的图象与坐标轴有交点,函数有零点.

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案【题目】有甲、乙两个班级进行数学考试,按照大于或等于90分为优秀,90分以下为非优秀统计成绩后,得到如表的列联表.
优秀 | 非优秀 | 总计 | |
甲班 | 10 | ||
乙班 | 30 | ||
合计 | 100 |
已知在全部100人中抽到随机抽取1人为优秀的概率为 ![]() .
.
(1)请完成如表的列联表;
(2)根据列联表的数据,有多大的把握认为“成绩与班级有关系“?
(3)按分层抽样的方法,从优秀学生中抽出6名组成一个样本,再从样本中抽出2名学生,求恰好有1个学生在甲班的概率.
参考公式和数据:K2= ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
下面的临界值表供参考:
p(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】电视传媒公司为了解某地区电视观众对里约奥运会的收视情况,随机抽取了100名观众进行调查,其中女性有55名,下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:
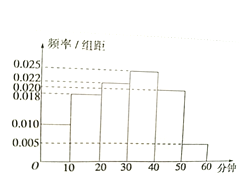
将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”。已知“体育迷”中有10名女性。
(1)试求“体育迷”中的男性观众人数;
(2)据此资料完成![]() 列联表,你是否认为“体育迷”与性别有关?
列联表,你是否认为“体育迷”与性别有关?
非体育迷 | 体育迷 | 合计 | |
男 | |||
女 | |||
合计 |
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
临界值表供参考参考公式: