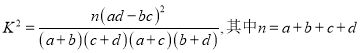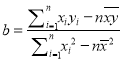题目内容
【题目】下列函数在其定义域中,既是奇函数又是增函数的( )
A.y=x+1
B.y=﹣x2
C.y=x|x|
D.![]()
【答案】C
【解析】解:因y=x+1的图象不关于原点对称,所以不是奇函数,不符合题意;
y=﹣x2在定义域R上为偶函数,不符合题意;
因函数y=x|x|的定义域为R,且(﹣x)|﹣x|=﹣x|x|,所以为奇函数,
又y=x|x|= ![]() ,则函数y=x|x|在[0,+∞),(﹣∞,0)上单调递增,
,则函数y=x|x|在[0,+∞),(﹣∞,0)上单调递增,
∵02=﹣02 , ∴该函数在定义域R上是增函数,符合题意;
由于函数y=﹣ ![]() 是奇函数,但在定义域(﹣∞,0)∪(0,+∞)上不是增函数,不符合题意.
是奇函数,但在定义域(﹣∞,0)∪(0,+∞)上不是增函数,不符合题意.
故选C.
利用函数奇偶性的定义判断各个选项中的函数的奇偶性,化简后由基本初等函数的单调性,判断函数在定义域上的单调性,从而得出答案.

练习册系列答案
相关题目
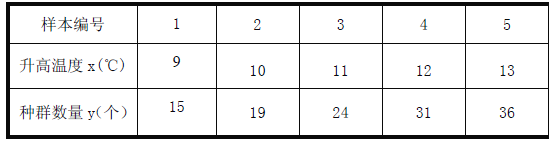
【题目】电视传媒公司为了解某地区电视观众对里约奥运会的收视情况,随机抽取了100名观众进行调查,其中女性有55名,下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:
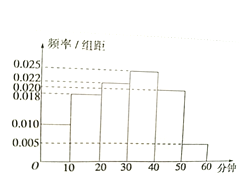
将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”。已知“体育迷”中有10名女性。
(1)试求“体育迷”中的男性观众人数;
(2)据此资料完成![]() 列联表,你是否认为“体育迷”与性别有关?
列联表,你是否认为“体育迷”与性别有关?
非体育迷 | 体育迷 | 合计 | |
男 | |||
女 | |||
合计 |
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
临界值表供参考参考公式: