Question

【题目】在平面直角坐标系xOy 中，椭圆G的中心为坐标原点，左焦点为F1（﹣1，0），离心率e=．

（1）求椭圆G 的标准方程；

（2）已知直线l1：y=kx+m1与椭圆G交于 A，B两点，直线l2：y=kx+m2（m1≠m2）与椭圆G交于C，D两点，且|AB|=|CD|，如图所示．

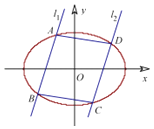
①证明：m1+m2=0；

②求四边形ABCD 的面积S 的最大值．

Answer 1

【答案】（1） （2）①见解析②

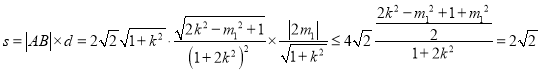【解析】试题分析：（1）由焦点坐标及离心率可求得，即可求椭圆G 的标准方程；（2）①利用弦长公式及韦达定理，表示出由，由得到；②四边形是平行四边形，设间的距离，由得，即可.

试题解析：（1）设椭圆G的方程为（a＞b＞0）

∵左焦点为F1（﹣1，0），离心率e=．∴c=1，a=，

b2=a2﹣c2=1

椭圆G 的标准方程为：．

（2）设A（x1，y1），B（x2，y2），C（x3，y3），D（x4，y4）

①证明：由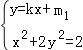消去y得（1+2k2）x2+4km1x+2m12﹣2=0

，

x1+x2=，x1x2=；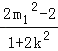

|AB|==2；

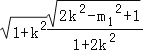同理|CD|=2，

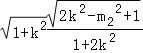由|AB|=|CD|得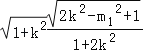2=2，

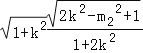∵m1≠m2，∴m1+m2=0

②四边形ABCD 是平行四边形，设AB，CD间的距离d=

∵m1+m2=0，∴

∴s=|AB|×d=2×

=.

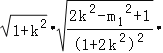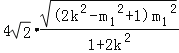
所以当2k2+1=2m12时，四边形ABCD 的面积S 的最大值为2