题目内容
如图,F1,F2是离心率为
的椭圆C:
+
=1(a>b>0)的左、右焦点,直线l:x=-
将线段F1F2分成两段,其长度之比为1:3.设A,B是C上的两个动点,线段AB的中垂线与C交于P,Q两点,线段AB的中点M在直线l上.
(Ⅰ)求椭圆C的方程;
(Ⅱ)求
•
的取值范围.

| ||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)求
| F2P |
| F2Q |

(Ⅰ)设F2(c,0),则
=
,所以c=1.
因为离心率e=
,所以a=
,所以b=1
所以椭圆C的方程为
+y2=1.…(6分)
(Ⅱ)当直线AB垂直于x轴时,直线AB方程为x=-
,此时P(-
,0)、Q(
,0),
•
=-1.
当直线AB不垂直于x轴时,设直线AB的斜率为k,M(-
,m)(m≠0),A(x1,y1),B(x2,y2).
由
得(x1+x2)+2(y1+y2)•
=0,
则-1+4mk=0,∴k=
.
此时,直线PQ斜率为k1=-4m,PQ的直线方程为y-m=-4m(x+
),即y=-4mx-m.
联立
消去y,整理得(32m2+1)x2+16m2x+2m2-2=0.
所以x1+x2=-
,x1x2=
.
于是
•
=(x1-1)(x2-1)+y1y2=x1x2-(x1+x2)+1+(4mx1+m)(4mx2+m)
=(1+16m2)x1x2+(4m2-1)(x1+x2)+1+m2
=
+
+1+m2=
.
令t=1+32m2,1<t<29,则
•
=
-
.
又1<t<29,所以-1<
•
<
.
综上,
•
的取值范围为[-1,
).…(15分)

c-
| ||
c+
|
| 1 |
| 3 |
因为离心率e=
| ||
| 2 |
| 2 |
所以椭圆C的方程为
| x2 |
| 2 |
(Ⅱ)当直线AB垂直于x轴时,直线AB方程为x=-
| 1 |
| 2 |
| 2 |
| 2 |
| F2P |
| F2Q |
当直线AB不垂直于x轴时,设直线AB的斜率为k,M(-
| 1 |
| 2 |
由
|
| y1-y2 |
| x1-x2 |
则-1+4mk=0,∴k=
| 1 |
| 4m |
此时,直线PQ斜率为k1=-4m,PQ的直线方程为y-m=-4m(x+
| 1 |
| 2 |
联立
|
所以x1+x2=-
| 16m2 |
| 32m2+1 |
| 2m2-2 |
| 32m2+1 |
于是
| F2P |
| F2Q |
=(1+16m2)x1x2+(4m2-1)(x1+x2)+1+m2
=
| (1+16m2)(2m2-2) |
| 32m2+1 |
| (4m2-1)(-16m2) |
| 32m2+1 |
| 19m2-1 |
| 32m2+1 |
令t=1+32m2,1<t<29,则
| F2P |
| F2Q |
| 19 |
| 32 |
| 51 |
| 32t |
又1<t<29,所以-1<
| F2P |
| F2Q |
| 125 |
| 232 |
综上,
| F2P |
| F2Q |
| 125 |
| 232 |


练习册系列答案
相关题目
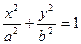 (a>b>0),A、B是椭圆上的两点,线段AB的垂直平分线与x轴相交于点P(x0,0).证明
(a>b>0),A、B是椭圆上的两点,线段AB的垂直平分线与x轴相交于点P(x0,0).证明 .
.