题目内容
已知椭圆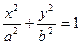 (a>b>0),A、B是椭圆上的两点,线段AB的垂直平分线与x轴相交于点P(x0,0).证明
(a>b>0),A、B是椭圆上的两点,线段AB的垂直平分线与x轴相交于点P(x0,0).证明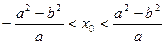 .
.
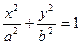 (a>b>0),A、B是椭圆上的两点,线段AB的垂直平分线与x轴相交于点P(x0,0).证明
(a>b>0),A、B是椭圆上的两点,线段AB的垂直平分线与x轴相交于点P(x0,0).证明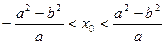 .
.证明见解析
本小题考查椭圆性质、直线方程等知识,以及综合分析能力.
证法一:设A、B的坐标分别为(x1,y1)和(x2,y2).因线段AB的垂直平分线与x轴相交,故AB不平行于y轴,即x1≠x2.又交点为P(x0,0),故|PA|=|PB|,即
(x1-x0)2+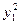 =(x2-x0)2+
=(x2-x0)2+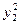 ①
①
∵ A、B在椭圆上,∴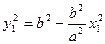 ,
,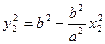 .
.
将上式代入①,得2(x2-x1) x0=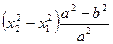 ②
②
∵ x1≠x2,可得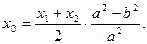 ③
③
∵ -a≤x1≤a,-a≤x2≤a,且x1≠x2,∴ -2a<x1+x2<2a,
∴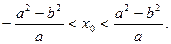
证法二:设A、B的坐标分别为(x1,y1)和(x2,y2).因P(x0,0)在AB的垂直平分线上,以点P为圆心,|PA|=r为半径的圆P过A、B两点,圆P的方程为(x-x0)2+y2=r2,
与椭圆方程联立,消去y得(x-x0)2 x2=r2-b2,
x2=r2-b2,
∴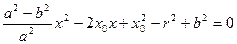 ①
①
因A、B是椭圆与圆P的交点,故x1,x2为方程①的两个根.由韦达定理得
x1+x2=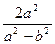 x0.
x0.
因-a≤x1≤a,-a≤x2≤a,且x1≠x2,故-2a<x1+x2=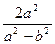 x0<2a,
x0<2a,
∴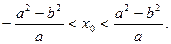
证法一:设A、B的坐标分别为(x1,y1)和(x2,y2).因线段AB的垂直平分线与x轴相交,故AB不平行于y轴,即x1≠x2.又交点为P(x0,0),故|PA|=|PB|,即
(x1-x0)2+
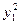 =(x2-x0)2+
=(x2-x0)2+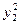 ①
①∵ A、B在椭圆上,∴
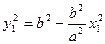 ,
,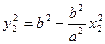 .
.将上式代入①,得2(x2-x1) x0=
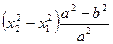 ②
②∵ x1≠x2,可得
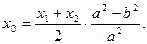 ③
③∵ -a≤x1≤a,-a≤x2≤a,且x1≠x2,∴ -2a<x1+x2<2a,
∴
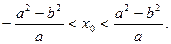
证法二:设A、B的坐标分别为(x1,y1)和(x2,y2).因P(x0,0)在AB的垂直平分线上,以点P为圆心,|PA|=r为半径的圆P过A、B两点,圆P的方程为(x-x0)2+y2=r2,
与椭圆方程联立,消去y得(x-x0)2
 x2=r2-b2,
x2=r2-b2,∴
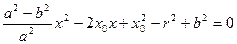 ①
①因A、B是椭圆与圆P的交点,故x1,x2为方程①的两个根.由韦达定理得
x1+x2=
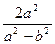 x0.
x0.因-a≤x1≤a,-a≤x2≤a,且x1≠x2,故-2a<x1+x2=
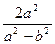 x0<2a,
x0<2a,∴
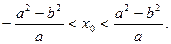

练习册系列答案
相关题目
 交椭圆
交椭圆 于
于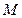 、
、 两点,椭圆与
两点,椭圆与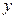 轴正半轴交于点
轴正半轴交于点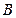 ,
,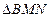 的重心恰好在椭圆的右焦点上,求直线
的重心恰好在椭圆的右焦点上,求直线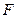 是椭圆的一个焦点,
是椭圆的一个焦点,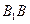 是短轴,
是短轴,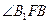
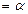 ,求这个椭圆的离心率。
,求这个椭圆的离心率。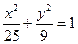 与曲线
与曲线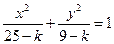
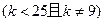 有相同的焦点。
有相同的焦点。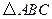 的顶点
的顶点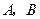 在椭圆
在椭圆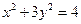 上,
上,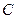 在直线
在直线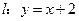 上,且
上,且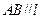 .
.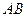 边通过坐标原点
边通过坐标原点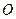 时,求
时,求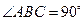 ,且斜边
,且斜边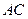 的长最大时,求
的长最大时,求
 (a>b>0)的左准线恰为抛物线E:y2 = 16x的准线,直线l:x + 2y – 4 = 0与椭圆相切.(1)求椭圆C的方程;(2)如果椭圆C的左顶点为A,右焦点为F,过F的直线与椭圆C交于P、Q两点,直线AP、AQ与椭圆C的右准线分别交于N、M两点,求证:四边形MNPQ的对角线的交点是定点.
(a>b>0)的左准线恰为抛物线E:y2 = 16x的准线,直线l:x + 2y – 4 = 0与椭圆相切.(1)求椭圆C的方程;(2)如果椭圆C的左顶点为A,右焦点为F,过F的直线与椭圆C交于P、Q两点,直线AP、AQ与椭圆C的右准线分别交于N、M两点,求证:四边形MNPQ的对角线的交点是定点.
 与定点
与定点 的距离和它到直线
的距离和它到直线 的距离的比是
的距离的比是 ,求点
,求点