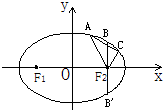
题目内容
已知椭圆C:
+
=1(a>b>0),过点A
,B
的直线倾斜角为
,原点到该直线的距离为
,求椭圆的方程.
| x2 |
| a2 |
| y2 |
| b2 |
|
|
| π |
| 6 |
| ||
| 2 |
过点A
,B
的直线方程为
+
=1,化为bx-ay+ab=0.
∵过点A
,B
的直线倾斜角为
,∴
=tan
=
.
又原点到该直线的距离为
,∴
=
,
联立
,解得
.
∴椭圆C的方程为
+y2=1.
|
|
| x |
| -a |
| y |
| b |
∵过点A
|
|
| π |
| 6 |
| b |
| a |
| π |
| 6 |
| ||
| 3 |
又原点到该直线的距离为
| ||
| 2 |
| ab | ||
|
| ||
| 2 |
联立
|
|
∴椭圆C的方程为
| x2 |
| 3 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 是椭圆的一个焦点,
是椭圆的一个焦点, 是短轴,
是短轴,
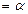 ,求这个椭圆的离心率。
,求这个椭圆的离心率。 (a>b>0)的左准线恰为抛物线E:y2 = 16x的准线,直线l:x + 2y – 4 = 0与椭圆相切.(1)求椭圆C的方程;(2)如果椭圆C的左顶点为A,右焦点为F,过F的直线与椭圆C交于P、Q两点,直线AP、AQ与椭圆C的右准线分别交于N、M两点,求证:四边形MNPQ的对角线的交点是定点.
(a>b>0)的左准线恰为抛物线E:y2 = 16x的准线,直线l:x + 2y – 4 = 0与椭圆相切.(1)求椭圆C的方程;(2)如果椭圆C的左顶点为A,右焦点为F,过F的直线与椭圆C交于P、Q两点,直线AP、AQ与椭圆C的右准线分别交于N、M两点,求证:四边形MNPQ的对角线的交点是定点.