题目内容
已知椭圆C的中心在原点,离心率等于
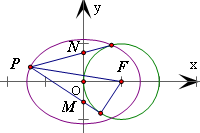
,右焦点F是圆(x-1)2+y2=1的圆心,过椭圆上位于y轴左侧的一动点P作该圆的两条切线分别交y轴于M、N两点.
(Ⅰ)求椭圆C的方程;
(Ⅱ)求线段MN的长的最大值,并求出此时点P的坐标.
| 2 |
| 3 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)求线段MN的长的最大值,并求出此时点P的坐标.
(I)设椭圆C的方程为
+
=1(a>b>0)
∵椭圆C的右焦点F是圆(x-1)2+y2=1的圆心F(1,0),
∴c=1,结合离心率e=
=
,得a=
因此,b2=a2-c2=
,得椭圆C的方程为
+
=1;
(II)设P(x0,y0),M(0,m),N(0,n),
可得直线PM的方程:y-m=
x,
化简得(y0-m)x-x0y+x0m=0.
又圆心(1,0)到直线PM的距离为1,
∴
=1,
平方化简得(y0-m)2+x02=(y0-m)2+2x0m(y0-m)+x02m2,
整理可得(x0-2)m2+2y0m-x0=0,同理可得(x0-2)n2+2y0n-x0=0.
因此,m、n是方程(x0-2)t2+2y0t-x0=0的两个不相等的实数根
∴m+n=
,mn=
,
∴|MN|=|m-n|=
=
.
∵P(x0,y0)是椭圆
+
=1上的点,
∴
+
=1,可得y02=
(1-
)=
-
x02
因此,|MN|=
=
,
记F(x0)=
,得F'(x)=
∵椭圆上动点P位于y轴左侧,可得x0∈[-
,0),而-
≤x0<0时F'(x)=
<0
∴F(x0)是上的减函数,可得F(x0)的最大值为F(-
)=
,此时|MN|=
因此线段MN的长的最大值为
,出此时点P的坐标为(-
,0).
| x2 |
| a2 |
| y2 |
| b2 |
∵椭圆C的右焦点F是圆(x-1)2+y2=1的圆心F(1,0),
∴c=1,结合离心率e=
| c |
| a |
| 2 |
| 3 |
| 3 |
| 2 |
因此,b2=a2-c2=
| 5 |
| 4 |
| x2 | ||
|
| y2 | ||
|
(II)设P(x0,y0),M(0,m),N(0,n),
可得直线PM的方程:y-m=
| y0-m |
| x0 |
化简得(y0-m)x-x0y+x0m=0.
又圆心(1,0)到直线PM的距离为1,
∴
| |y0-m+x0m| | ||
|
平方化简得(y0-m)2+x02=(y0-m)2+2x0m(y0-m)+x02m2,
整理可得(x0-2)m2+2y0m-x0=0,同理可得(x0-2)n2+2y0n-x0=0.
因此,m、n是方程(x0-2)t2+2y0t-x0=0的两个不相等的实数根
∴m+n=
| -2y0 |
| x0-2 |
| -x0 |
| x0-2 |
∴|MN|=|m-n|=
| (m+n)2-4mn |
|
∵P(x0,y0)是椭圆
| x2 | ||
|
| y2 | ||
|
∴
| x02 | ||
|
| y02 | ||
|
| 5 |
| 4 |
| x02 | ||
|
| 5 |
| 4 |
| 5 |
| 9 |
因此,|MN|=
|
|
记F(x0)=
| ||
| (x0-2)2 |
| ||
| (x0-2)3 |
∵椭圆上动点P位于y轴左侧,可得x0∈[-
| 3 |
| 2 |
| 3 |
| 2 |
| ||
| (x0-2)3 |
∴F(x0)是上的减函数,可得F(x0)的最大值为F(-
| 3 |
| 2 |
| 12 |
| 7 |
2
| ||
| 7 |
因此线段MN的长的最大值为
2
| ||
| 7 |
| 3 |
| 2 |


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
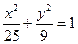 与曲线
与曲线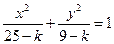
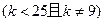 有相同的焦点。
有相同的焦点。