题目内容
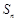 是数列
是数列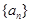 的前
的前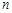 项和,则“数列
项和,则“数列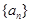 为常数列”是“数列
为常数列”是“数列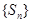 为等差数列”的
为等差数列”的| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
A
分析:先看如果数列{Sn}为等差数列成立能不能得出“数列{an}为常数列”成立,如果成立则为充分条件;同理看如果“数列{an}为常数列”成立能不能退出“数列{Sn}为等差数列”,如果成立则“数列{Sn}为等差数列”是“数列{an}为常数列”必要条件.
解:如果数列{Sn}为等差数列,
an+1=Sn+1-Sn=p,则p为常数,故数列{an}为常数列
∴“数列{an}为常数列”是“数列{Sn}为等差数列”的充分条件
如果a(n)是常数列,当限制n的取值范围时,s(n)就不是等差数列.
∴“数列{an}为常数列”是“数列{Sn}为等差数列”的不必要条件.
故选A

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
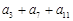 为一个确定的常数,则下列各数中也是常数的是( )
为一个确定的常数,则下列各数中也是常数的是( )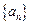 满足
满足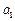 =0,
=0,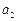 =2,
=2,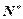 都有
都有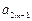 +
+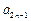 =
=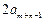 +
+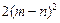
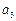 ,
,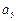 ;
;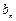 =
=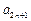 -
-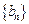 是等差数列;
是等差数列;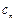 =(
=(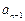 -
-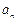 )
)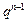 ( q≠0,n∈
( q≠0,n∈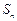 .
.
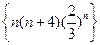 中的最大项是第
中的最大项是第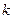 项,则
项,则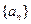 中,
中,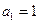 ,点
,点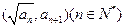 在函数
在函数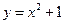 的图象上,数列
的图象上,数列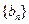 的前n项和
的前n项和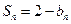 .
.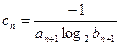 ,求
,求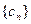 的前n项和
的前n项和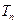 .
.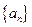 的前n项和为
的前n项和为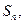 已知
已知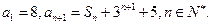
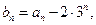 证明:数列
证明:数列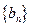 是等比数列;
是等比数列;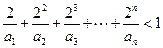 .
.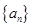 的通项公式是
的通项公式是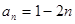 ,其前n项和为
,其前n项和为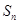 ,则数列
,则数列 的
的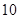 项和为( )
项和为( )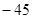
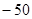
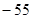
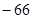
 ).
).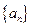 中,
中,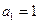 ,
,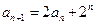 .
.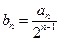 .证明:数列
.证明:数列 是等差数列;
是等差数列;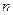 项和
项和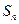 .
.