题目内容
(本小题满分16分)设数列{an}满足:a1=1,a2=2,an+2=(n≥1,n∈N* ).
).
(1) 求证:数列是常数列;
(2) 求证:当n≥2时,2<a-a≤3;
(3) 求a2 011的整数部分.
 ).
).(1) 求证:数列是常数列;
(2) 求证:当n≥2时,2<a-a≤3;
(3) 求a2 011的整数部分.
(1) 易知,对一切n≥1,an≠0,由an+2=,得=.
依次利用上述关系式,可得
===…===1,
从而数列是常数列.(4分)
(2) 由(1)得an+1=an+.
又a1=1,∴可知数列{an}递增,则 对一切n≥1,有an≥1成立,从而0<≤1.(6分)
对一切n≥1,有an≥1成立,从而0<≤1.(6分)
当n≥2时,a=2=a++2,
于是a-a=+2,
∴2<a-a≤3.(8分)
(3) 当n≥2时,a=a++2,
∴a=+…++a+2(n-1).
a=1,a=4,则当n≥3时,
a=+…++a+2(n-1)
=+…++1+1+2(n-1)
=+…++2n>2n.
a=+…++2(2 011-1)+1>4 021
>3 969=632,(10分)
a=+…++2(2 011-1)+1
=4 021++…+
<4 020++++…+
=4 022+
=4 022+
]
<4 022+
]
=4 022+
<4 022+(19+4+10)<4 039<4 096=642.(14分)
∴63<a2 011<64,即a2 011的整数部分为63.(16分)
依次利用上述关系式,可得
===…===1,
从而数列是常数列.(4分)
(2) 由(1)得an+1=an+.
又a1=1,∴可知数列{an}递增,则
 对一切n≥1,有an≥1成立,从而0<≤1.(6分)
对一切n≥1,有an≥1成立,从而0<≤1.(6分)当n≥2时,a=2=a++2,
于是a-a=+2,
∴2<a-a≤3.(8分)
(3) 当n≥2时,a=a++2,
∴a=+…++a+2(n-1).
a=1,a=4,则当n≥3时,
a=+…++a+2(n-1)
=+…++1+1+2(n-1)
=+…++2n>2n.
a=+…++2(2 011-1)+1>4 021
>3 969=632,(10分)
a=+…++2(2 011-1)+1
=4 021++…+
<4 020++++…+
=4 022+
=4 022+
]
<4 022+
]
=4 022+

<4 022+(19+4+10)<4 039<4 096=642.(14分)
∴63<a2 011<64,即a2 011的整数部分为63.(16分)
略

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
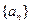 的前
的前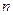 项和为
项和为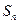 ,且
,且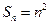 .数列
.数列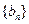 为等比数列,且
为等比数列,且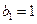 ,
,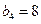 .
.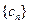 满足
满足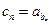 ,求数列
,求数列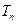 ;
;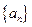 的前
的前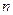 项和为
项和为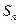 ,已知
,已知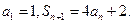
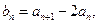 证明数列
证明数列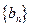 是等比数列;
是等比数列;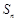 是数列
是数列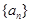 的前
的前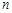 项和,则“数列
项和,则“数列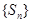 为等差数列”的
为等差数列”的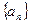 的各项均为正数,
的各项均为正数,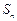 为其前
为其前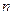 项和,对于任意
项和,对于任意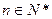 ,总有
,总有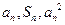 成等差数列.
成等差数列.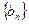 的前
的前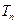 ,且
,且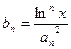 ,求证:对任意实数
,求证:对任意实数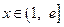 (
(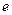 是常数,
是常数,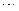 )和任意正整数
)和任意正整数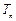
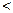 2;
2;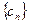 中,
中,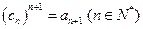 .,求数列
.,求数列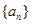 的前n项和为
的前n项和为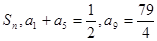 ,则S11= ( )
,则S11= ( )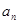 }中共有18项,其中奇数项之和为11,偶数项之和为29,则其公差为( )
}中共有18项,其中奇数项之和为11,偶数项之和为29,则其公差为( )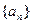 为等差数列,
为等差数列,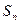 为数列
为数列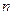 项和,已知
项和,已知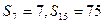 ,求数列
,求数列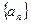 中,
中,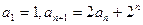
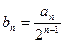 ,证明:数列
,证明:数列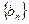 是等差数列;
是等差数列;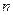 项和
项和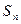 .
.