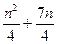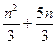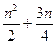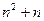题目内容
(本小题满分16分)
已知数列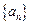 满足
满足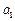 =0,
=0,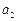 =2,
=2,
且对任意m,n∈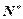 都有
都有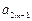 +
+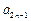 =
=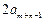 +
+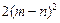
(1)求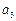 ,
,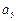 ;
;
(2)设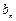 =
=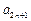 -
-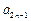 ( n∈
( n∈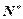 ),证明:
),证明: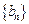 是等差数列;
是等差数列;
(3)设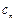 =(
=(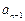 -
-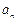 )
)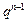 ( q≠0,n∈
( q≠0,n∈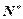 ),求数列的前n项的和
),求数列的前n项的和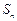 .
.
已知数列
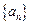 满足
满足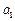 =0,
=0,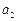 =2,
=2,且对任意m,n∈
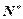 都有
都有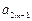 +
+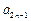 =
=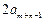 +
+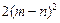
(1)求
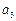 ,
,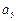 ;
;(2)设
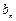 =
=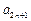 -
-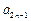 ( n∈
( n∈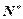 ),证明:
),证明: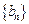 是等差数列;
是等差数列;(3)设
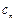 =(
=(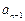 -
-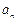 )
)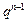 ( q≠0,n∈
( q≠0,n∈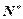 ),求数列的前n项的和
),求数列的前n项的和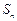 .
.解析:(1)由题意,令m=2,n=1,可得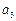 =
= -
-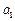 +2=6,再令m=3,n=1,可得
+2=6,再令m=3,n=1,可得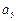 =
=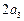 -
-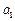 +8=20.
+8=20.
(2)当n∈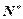 时,由已知(以n+2代替m)可得
时,由已知(以n+2代替m)可得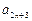 +
+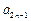 =
=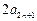 +8,于是[
+8,于是[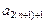 -
-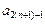 ]-(
]-(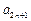 -
-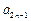 )=8,即
)=8,即 -
-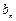 =8.所以
=8.所以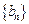 是公差为8的等差数列.
是公差为8的等差数列.
(3)由(1)(2)可知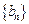 是首项
是首项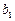 =
=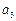 -
-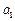 =6,公差为8的等差数列,则
=6,公差为8的等差数列,则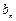 =8n-2,即
=8n-2,即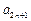 -
-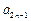 =8n-2.另由已知(令m=1)可得,
=8n-2.另由已知(令m=1)可得,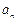 =
=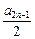 -
-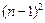 .那么
.那么
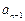 -
-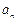 =
=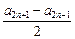 -2n+1=
-2n+1=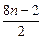 -2n+1=2n,于是
-2n+1=2n,于是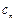 =
=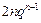 .
.
当q=1时,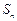 =2+4+6+…+2n=n (n+1).
=2+4+6+…+2n=n (n+1).
当q≠1时,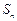 =2·
=2·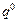 +4·
+4·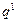 +6·
+6·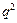 +…+2n·
+…+2n·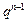 ,两边同乘以q,可得
,两边同乘以q,可得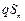 =2·
=2·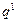 +4·
+4·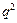 +6·
+6·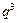 +…+2n·
+…+2n·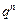 .上述两式相减,得
.上述两式相减,得
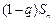 =
=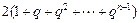 -2n
-2n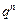 =
=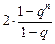 -2n
-2n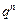 =
= ,
,
所以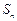 =
=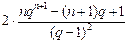 .
.
综上所述,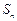 =
=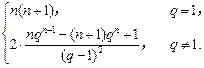
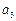 =
= -
-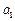 +2=6,再令m=3,n=1,可得
+2=6,再令m=3,n=1,可得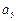 =
=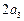 -
-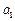 +8=20.
+8=20.(2)当n∈
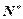 时,由已知(以n+2代替m)可得
时,由已知(以n+2代替m)可得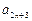 +
+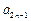 =
=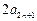 +8,于是[
+8,于是[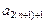 -
-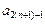 ]-(
]-(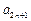 -
-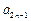 )=8,即
)=8,即 -
-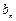 =8.所以
=8.所以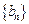 是公差为8的等差数列.
是公差为8的等差数列.(3)由(1)(2)可知
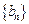 是首项
是首项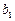 =
=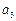 -
-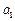 =6,公差为8的等差数列,则
=6,公差为8的等差数列,则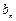 =8n-2,即
=8n-2,即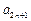 -
-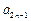 =8n-2.另由已知(令m=1)可得,
=8n-2.另由已知(令m=1)可得,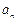 =
=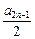 -
-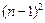 .那么
.那么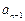 -
-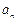 =
=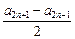 -2n+1=
-2n+1=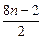 -2n+1=2n,于是
-2n+1=2n,于是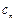 =
=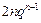 .
.当q=1时,
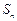 =2+4+6+…+2n=n (n+1).
=2+4+6+…+2n=n (n+1).当q≠1时,
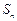 =2·
=2·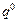 +4·
+4·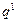 +6·
+6·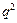 +…+2n·
+…+2n·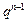 ,两边同乘以q,可得
,两边同乘以q,可得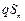 =2·
=2·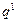 +4·
+4·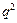 +6·
+6·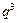 +…+2n·
+…+2n·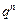 .上述两式相减,得
.上述两式相减,得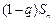 =
=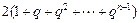 -2n
-2n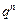 =
=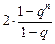 -2n
-2n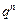 =
= ,
,所以
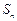 =
=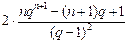 .
.综上所述,
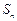 =
=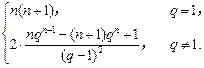
略

练习册系列答案
相关题目
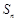 是数列
是数列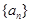 的前
的前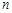 项和,则“数列
项和,则“数列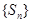 为等差数列”的
为等差数列”的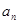 }中共有18项,其中奇数项之和为11,偶数项之和为29,则其公差为( )
}中共有18项,其中奇数项之和为11,偶数项之和为29,则其公差为( )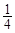
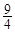
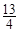
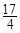 、
、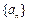 的公差为负数,且
的公差为负数,且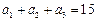 ,若
,若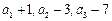 经重新排列后依次可成等比数列,求⑴数列
经重新排列后依次可成等比数列,求⑴数列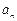 ;⑵数列
;⑵数列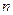 项和
项和 的最大值。
的最大值。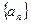 中,
中,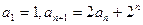
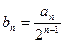 ,证明:数列
,证明:数列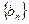 是等差数列;
是等差数列;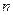 项和
项和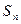 .
.
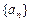 的公差是3,若
的公差是3,若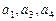 成等比数列,则
成等比数列,则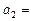 ________________
________________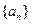 是公差不为0的等差数列,
是公差不为0的等差数列,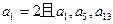 成等比数列,则数列
成等比数列,则数列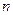 项和
项和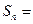 ( )
( )