题目内容
12．已知公差不为零的等差数列{an}与公比为q的等比数列{bn}有相同的首项，同时满足a1，a4，b3成等比，b1，a3，b3成等差，则q2=（ ）| A． | $\frac{1}{4}$ | B． | $\frac{1}{6}$ | C． | $\frac{1}{9}$ | D． | $\frac{1}{8}$ |
分析 设等差数列{an}的公差为d（d≠0），由a1=b1，结合a1，a4，b3成等比，b1，a3，b3成等差列式求得答案．
解答 解：设等差数列{an}的公差为d（d≠0），且a1=b1，
由a1，a4，b3成等比，b1，a3，b3成等差，得
$（{a}_{1}+3d）^{2}={a}_{1}{b}_{1}{q}^{2}$ ①，
$2（{a}_{1}+2d）={b}_{1}+{b}_{1}{q}^{2}$ ②，
又a1=b1，
解得：${q}^{2}=\frac{1}{9}$．
故选：C．
点评 本题考查等差数列和等比数列的通项公式，是基础的计算题．
练习册系列答案
名校课堂系列答案
相关题目
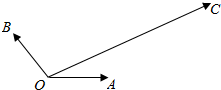如图，|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1，$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为120°，$\overrightarrow{OC}$与$\overrightarrow{OA}$的夹角为30°，|$\overrightarrow{OC}$|=2$\sqrt{3}$，用$\overrightarrow{OA}$、$\overrightarrow{OB}$表示$\overrightarrow{OC}$为$\overrightarrow{OC}$=4$\overrightarrow{OA}$+2$\overrightarrow{OB}$．
17．下列函数为奇函数的是 （ ）
| A． | y=-|x| | B． | y=2-x | C． | y=$\frac{1}{{x}^{3}}$ | D． | y=-x2+8 |