题目内容
函数f(x)=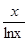 的单调递减区间是
的单调递减区间是
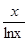 的单调递减区间是
的单调递减区间是 (0,1),(1,e)
解:因为x>0,那么求解导数f’(x)=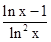 ,可知当x=e,f’(x)=0,那么利用导数的符号与函数单调性的关系可知,函数的递减区间为(0,1),(1,e)。
,可知当x=e,f’(x)=0,那么利用导数的符号与函数单调性的关系可知,函数的递减区间为(0,1),(1,e)。
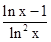 ,可知当x=e,f’(x)=0,那么利用导数的符号与函数单调性的关系可知,函数的递减区间为(0,1),(1,e)。
,可知当x=e,f’(x)=0,那么利用导数的符号与函数单调性的关系可知,函数的递减区间为(0,1),(1,e)。
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 在点
在点 的切线方程为
的切线方程为 .
. 的解析式;
的解析式; ,求证:
,求证: 在
在 上恒成立.
上恒成立.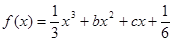 的图象在点
的图象在点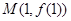 处的切线方程为
处的切线方程为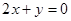 。
。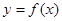 的解析式;
的解析式;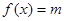 在区间
在区间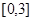 上恰有两个相异实根,求m的取值范围。
上恰有两个相异实根,求m的取值范围。 ,其中a为实数。
,其中a为实数。 的单调区间;
的单调区间; 对定义域内的任意x恒成立,求实数a的取值范围。
对定义域内的任意x恒成立,求实数a的取值范围。 恒成立。
恒成立。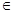 R为常数.
R为常数. 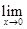
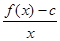 =4,试证:-6≤b≤2.
=4,试证:-6≤b≤2. 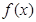 ,若满足
,若满足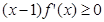 ,则必有( )
,则必有( )
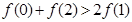
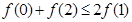 D.
D. 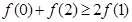
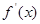 是函数
是函数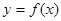 的导函数,且
的导函数,且 的图像如图所示,
的图像如图所示,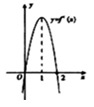
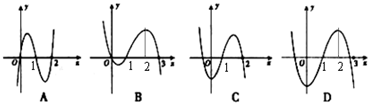

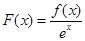 是定义在R上的函数,其中
是定义在R上的函数,其中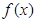 的导函数为
的导函数为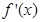 ,满足
,满足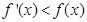 对于
对于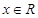 恒成立,则( )
恒成立,则( )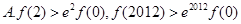


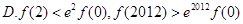
 ,-1)上为增函数,在(-1,1)上为减函数,则f(1)为( )
,-1)上为增函数,在(-1,1)上为减函数,则f(1)为( )