题目内容
【题目】如图，矩形草坪AMPN中，点C在对角线MN上．CD垂直于AN于点D，CB垂直于AM于点B，|CD|=|AB|=3米，|AD|=|BC|=2米，设|DN|=x米，|BM|=y米．求这块矩形草坪AMPN面积的最小值．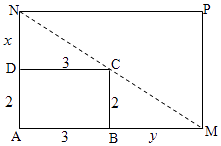 
【答案】解：由题意 
．
SAMPN=（x+2）（y+3）=xy+3x+2y+6=12+3x+2y．
．
当且仅当3x=2y，即x=2，y=3时取得等号．．
面积的最小值为24平方米．
【解析】由题意 
，表示出矩形的面积，利用基本不等式，即可求得结论．
【考点精析】关于本题考查的基本不等式在最值问题中的应用，需要了解用基本不等式求最值时（积定和最小，和定积最大），要注意满足三个条件“一正、二定、三相等”才能得出正确答案．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
