题目内容
【题目】定义函数 ![]() ,其中x为自变量,a为常数. (I)若当x∈[0,2]时,函数fa(x)的最小值为一1,求a之值;
,其中x为自变量,a为常数. (I)若当x∈[0,2]时,函数fa(x)的最小值为一1,求a之值;
(II)设全集U=R,集A={x|f3(x)≥fa(0)},B={x|fa(x)+fa(2﹣x)=f2(2)},且(UA)∩B≠中,求a的取值范围.
【答案】解:(Ⅰ)令t=2x,∵x∈[0,2],∴t∈[1,4],
设φ(t)=t2﹣(a+1)t+a,t∈[1,4]
1°当 ![]() ,即a≤1时,fmin(x)=φ(1)=0,与已知矛盾;
,即a≤1时,fmin(x)=φ(1)=0,与已知矛盾;
2°当 ![]() ,即
,即 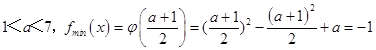 ,
,
解得a=3或a=﹣1,∵1<a<7,∴a=3;
3°当 ![]() ,即a≥7,fmin(x)=φ(4)=16﹣4a﹣4+a=1,
,即a≥7,fmin(x)=φ(4)=16﹣4a﹣4+a=1,
解得 ![]() ,但与a≥7矛盾,故舍去
,但与a≥7矛盾,故舍去
综上所述,a之值为3
(Ⅱ)UA={x|4x﹣42x+3<0}={x|0<x<log23}
B={x|4x﹣(a+1)2x+a+42﹣x﹣(a+1)22﹣x+a=6}= ![]() .
.
由已知(UA)∩B≠即 ![]() ﹣(a+1)(
﹣(a+1)( ![]() )+2a﹣6=0在(0,log23)内有解,
)+2a﹣6=0在(0,log23)内有解,
令t= ![]() ,则t∈[4,5),方程(t2﹣8)﹣(a+1)t+2a﹣6在[4,5)上有解,
,则t∈[4,5),方程(t2﹣8)﹣(a+1)t+2a﹣6在[4,5)上有解,
也等价于方程 ![]() 在t∈[4,5)上有解
在t∈[4,5)上有解
∵ ![]() 在t∈[4,5)上单调递增,
在t∈[4,5)上单调递增,
∴h(t)∈[﹣1,2)
故所求a的取值范围是[﹣1,2)
【解析】(I)若当x∈[0,2]时,换元,得到φ(t)=t2﹣(a+1)t+a,t∈[1,4],分类讨论,利用函数fa(x)的最小值为﹣1,求a之值;(II)令t= ![]() ,则t∈[4,5),方程(t2﹣8)﹣(a+1)t+2a﹣6在[4,5)上有解,也等价于方程
,则t∈[4,5),方程(t2﹣8)﹣(a+1)t+2a﹣6在[4,5)上有解,也等价于方程 ![]() 在t∈[4,5)上有解,利用基本不等式,即可求a的取值范围.
在t∈[4,5)上有解,利用基本不等式,即可求a的取值范围.
【考点精析】认真审题,首先需要了解集合的交集运算(交集的性质:(1)A∩B![]() A,A∩B
A,A∩B![]() B,A∩A=A,A∩
B,A∩A=A,A∩![]() =
=![]() ,A∩B=B∩A;(2)若A∩B=A,则A
,A∩B=B∩A;(2)若A∩B=A,则A![]() B,反之也成立),还要掌握函数的最值及其几何意义(利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值)的相关知识才是答题的关键.
B,反之也成立),还要掌握函数的最值及其几何意义(利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值)的相关知识才是答题的关键.

 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案