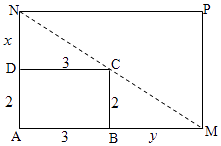
题目内容
【题目】已知{an}是各项均为正数的等比数列，{bn}是等差数列，且a1=b1=1，b2+b3=2a3 ， a5﹣3b2=7．
（1）求{an}和{bn}的通项公式；
（2）设cn=anbn ， n∈N* ， 求数列{cn}的前n项和．
【答案】
（1）解：设数列{an}的公比为q，数列{bn}的公差为d，由题意，q＞0，
由已知有 
，消去d整理得：q4﹣2q2﹣8=0．
∵q＞0，解得q=2，∴d=2，
∴数列{an}的通项公式为 
，n∈N*；
数列{bn}的通项公式为bn=2n﹣1，n∈N*．
（2）解：由（1）有 
，
设{cn}的前n项和为Sn，则
，
，
两式作差得： 
=2n+1﹣3﹣（2n﹣1）×2n=﹣（2n﹣3）×2n﹣3．
∴ 
【解析】（1）设出数列{an}的公比和数列{bn}的公差，由题意列出关于q，d的方程组，求解方程组得到q，d的值，则等差数列和等比数列的通项公式可求；（2）由题意得到 ，然后利用错位相减法求得数列{cn}的前n项和．
练习册系列答案
相关题目
