题目内容
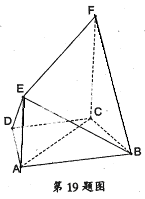
如图,在三棱锥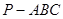 中,
中,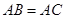 ,
,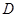 为
为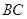 的中点,
的中点,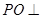 平面
平面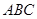 ,垂足
,垂足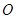 落在线段
落在线段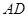 上,已知
上,已知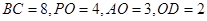 。
。
(Ⅰ)证明: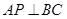 ;
;
(Ⅱ)在线段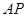 上是否存在点M,使得二面角
上是否存在点M,使得二面角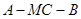 为直二面角?若存在,求
为直二面角?若存在,求
出AM的长;若不存在,请说明理由。(12分)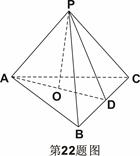
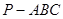 中,
中,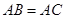 ,
,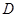 为
为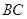 的中点,
的中点,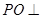 平面
平面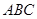 ,垂足
,垂足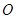 落在线段
落在线段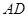 上,已知
上,已知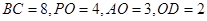 。
。(Ⅰ)证明:
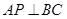 ;
;(Ⅱ)在线段
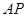 上是否存在点M,使得二面角
上是否存在点M,使得二面角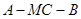 为直二面角?若存在,求
为直二面角?若存在,求出AM的长;若不存在,请说明理由。(12分)

见解析
第一问中,利用由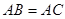 ,D是BC的中点,得
,D是BC的中点,得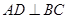 ,又
,又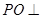 平面ABC,得
平面ABC,得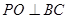 ,因为
,因为 ,所以
,所以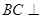 平面PAD,故
平面PAD,故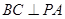 ‘利用线面垂直的性质定理得到。
‘利用线面垂直的性质定理得到。
第二问中,利用在平面PAB内作 于M,连接CM,由(1)中知
于M,连接CM,由(1)中知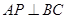 ,得
,得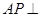 平面BMC,
平面BMC,
又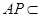 平面APC,所以平面
平面APC,所以平面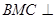 平面APC,在
平面APC,在 中,
中, ,得
,得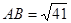 ,在
,在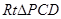 中,
中,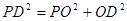 。
。
在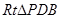 中,
中,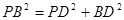 。
。
所以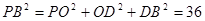 ,得
,得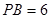
在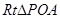 中,
中,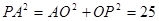 ,得
,得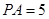
又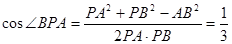 。
。
从而
所以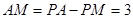 综上所述,存在点M符合题意AM=3
综上所述,存在点M符合题意AM=3
(1)证明:由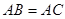 ,D是BC的中点,得
,D是BC的中点,得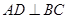 ,
,
又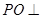 平面ABC,得
平面ABC,得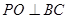 ,因为
,因为 ,
,
所以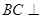 平面PAD,故
平面PAD,故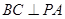 ………….4分
………….4分
(2)解:如图,在平面PAB内作 于M,连接CM,由(1)中知
于M,连接CM,由(1)中知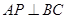 ,得
,得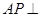 平面BMC,
平面BMC,
又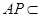 平面APC,所以平面
平面APC,所以平面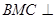 平面APC,……….6分,
平面APC,……….6分,
在 中,
中, ,得
,得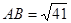 ,
,
在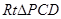 中,
中,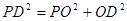 。
。
在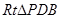 中,
中,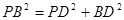 。
。
所以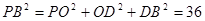 ,得
,得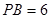
在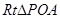 中,
中,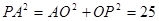 ,得
,得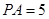
又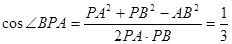 。
。
从而 ………….10分
………….10分
所以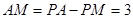
综上所述,存在点M符合题意AM=3。…………12分
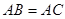 ,D是BC的中点,得
,D是BC的中点,得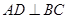 ,又
,又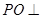 平面ABC,得
平面ABC,得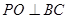 ,因为
,因为 ,所以
,所以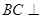 平面PAD,故
平面PAD,故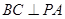 ‘利用线面垂直的性质定理得到。
‘利用线面垂直的性质定理得到。第二问中,利用在平面PAB内作
 于M,连接CM,由(1)中知
于M,连接CM,由(1)中知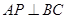 ,得
,得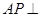 平面BMC,
平面BMC,又
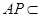 平面APC,所以平面
平面APC,所以平面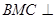 平面APC,在
平面APC,在 中,
中, ,得
,得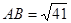 ,在
,在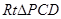 中,
中,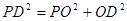 。
。在
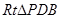 中,
中,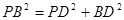 。
。所以
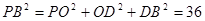 ,得
,得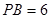
在
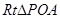 中,
中,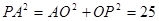 ,得
,得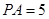
又
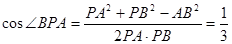 。
。从而

所以
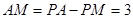 综上所述,存在点M符合题意AM=3
综上所述,存在点M符合题意AM=3(1)证明:由
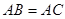 ,D是BC的中点,得
,D是BC的中点,得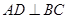 ,
,又
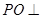 平面ABC,得
平面ABC,得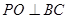 ,因为
,因为 ,
,所以
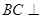 平面PAD,故
平面PAD,故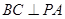 ………….4分
………….4分(2)解:如图,在平面PAB内作
 于M,连接CM,由(1)中知
于M,连接CM,由(1)中知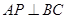 ,得
,得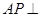 平面BMC,
平面BMC,又
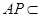 平面APC,所以平面
平面APC,所以平面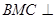 平面APC,……….6分,
平面APC,……….6分,在
 中,
中, ,得
,得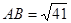 ,
,在
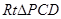 中,
中,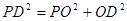 。
。在
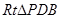 中,
中,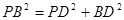 。
。所以
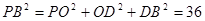 ,得
,得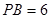
在
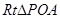 中,
中,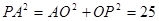 ,得
,得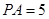
又
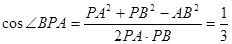 。
。从而
 ………….10分
………….10分所以
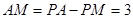
综上所述,存在点M符合题意AM=3。…………12分

练习册系列答案
相关题目
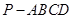 的底面是正方形,
的底面是正方形,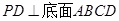 ,点E在棱PB上。
,点E在棱PB上。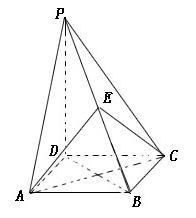
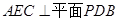 ;
;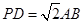 且E为PB的中点时,求AE与平
且E为PB的中点时,求AE与平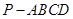 中,底面
中,底面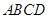 为矩形,
为矩形,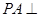 底面
底面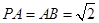 ,点
,点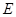 是棱
是棱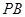 的中点.
的中点.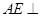 平面
平面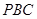 ;
;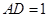 ,求二面角
,求二面角 的平面角的余弦值.
的平面角的余弦值. 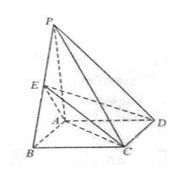
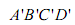 ,其中A与A '重合,且BB'<DD'<CC'.
,其中A与A '重合,且BB'<DD'<CC'.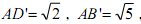 ,正方形的边长为
,正方形的边长为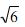 ,
, 的余弦值.
的余弦值.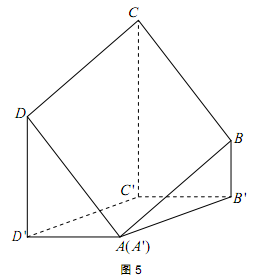
 中,
中, ="2" ,
="2" ,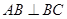 .点
.点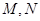 分别是
分别是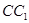 ,
,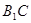 的中点,
的中点,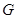 是棱
是棱 上的动点.
上的动点.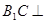 平面
平面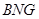 ;
;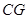 //平面
//平面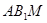 ,试确定
,试确定 的余弦值.
的余弦值.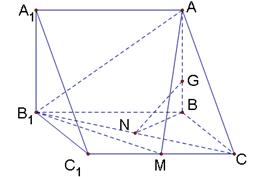 【
【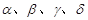 表示平面,
表示平面,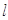 为直线,下列命题中为真命题的是 ( )
为直线,下列命题中为真命题的是 ( )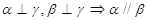
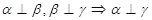
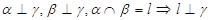
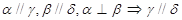
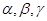 ,直线
,直线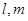 满足:
满足: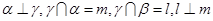 ,那么
,那么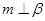 ; ②
; ②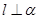 ; ③
; ③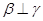 ; ④
; ④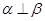 。
。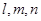 是三条不同的直线,
是三条不同的直线,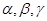 是三个不同的平面,现给出四个命题:
是三个不同的平面,现给出四个命题: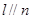 且
且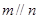 ,则
,则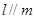 ; ②若
; ②若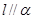 且
且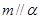 ,则
,则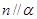 且
且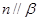 ,则
,则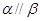 ; ④若
; ④若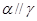 且
且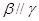 ,则
,则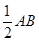 ,∠ACF=∠ADC=
,∠ACF=∠ADC=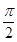 。
。