题目内容
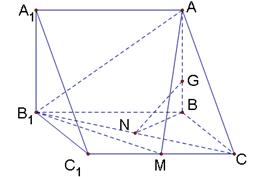
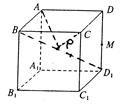
在直三棱柱 中,
中, ="2" ,
="2" ,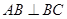 .点
.点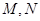 分别是
分别是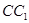 ,
,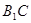 的中点,
的中点,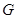 是棱
是棱 上的动点.
上的动点.
(I)求证: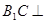 平面
平面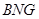 ;
;
(II)若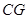 //平面
//平面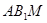 ,试确定
,试确定 点的位置,
点的位置,
并给出证明;
(III)求二面角 的余弦值.
的余弦值.
 【
【
 中,
中, ="2" ,
="2" ,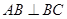 .点
.点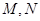 分别是
分别是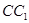 ,
,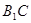 的中点,
的中点,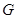 是棱
是棱 上的动点.
上的动点.(I)求证:
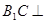 平面
平面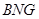 ;
;(II)若
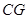 //平面
//平面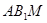 ,试确定
,试确定 点的位置,
点的位置,并给出证明;
(III)求二面角
 的余弦值.
的余弦值. 【
【(1)见解析;(2)见解析;(3)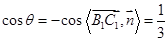 .
.
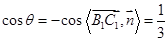 .
.本题考查了线面平行与垂直及二面角的求法。第一问抓住线面垂直的判定定理须证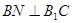 ,
,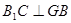 ;第二问先说明
;第二问先说明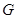 是棱
是棱 的中点,再,取
的中点,再,取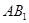 的中点H,证明四边形
的中点H,证明四边形 为平行四边形,由线面平行的判定定理得证;第三问利用法向量求二面角
为平行四边形,由线面平行的判定定理得证;第三问利用法向量求二面角 的余弦值,要注意法向量的准确求解和余弦值的正负。
的余弦值,要注意法向量的准确求解和余弦值的正负。
解:(I) 证明:∵在直三棱柱 中,
中,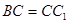 ,点
,点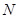 是
是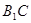 的中点,
的中点,
∴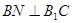 …………………………1分
…………………………1分
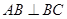 ,
, ,
,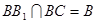
∴ ⊥平面
⊥平面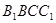 ………………………2分
………………………2分
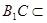 平面
平面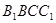
∴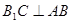 ,即
,即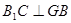 …………………3分
…………………3分
又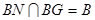
∴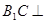 平面
平面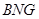 …………………………………4分
…………………………………4分
(II)当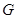 是棱
是棱 的中点时,
的中点时,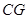 //平面
//平面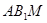 .……………………………5分
.……………………………5分
证明如下:
 连结
连结 ,取
,取 的中点H,连接
的中点H,连接 ,
,
则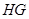 为
为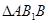 的中位线
的中位线
∴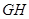 ∥
∥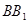 ,
,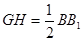 …………………6分
…………………6分
∵由已知条件,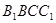 为正方形
为正方形
∴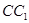 ∥
∥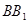 ,
,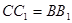
∵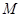 为
为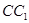 的中点,
的中点,
∴ ……………………7分
……………………7分
∴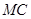 ∥
∥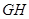 ,且
,且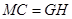
∴四边形 为平行四边形
为平行四边形
∴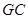 ∥
∥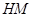
又 ∵
∴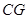 //平面
//平面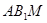 ……………………8分
……………………8分
(III)∵直三棱柱 且
且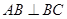
依题意,如图:以 为原点建立空间直角坐标系
为原点建立空间直角坐标系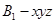 ,……………………9分
,……………………9分

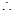
 ,
,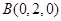 ,
,
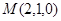
 ,
,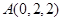 ,
,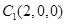
则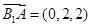 ,
,
设平面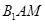 的法向量
的法向量 ,
,
则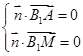 ,即
,即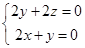 ,
,
令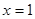 ,有
,有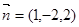 ……………………10分
……………………10分
又 平面
平面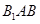 的法向量为
的法向量为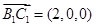 ,
,
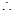
 =
= =
=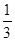 , ……………………11分
, ……………………11分
设二面角 的平面角为
的平面角为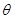 ,且
,且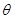 为锐角
为锐角
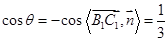 . ……………………12分.
. ……………………12分.
 ,
,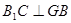 ;第二问先说明
;第二问先说明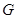 是棱
是棱 的中点,再,取
的中点,再,取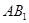 的中点H,证明四边形
的中点H,证明四边形 为平行四边形,由线面平行的判定定理得证;第三问利用法向量求二面角
为平行四边形,由线面平行的判定定理得证;第三问利用法向量求二面角 的余弦值,要注意法向量的准确求解和余弦值的正负。
的余弦值,要注意法向量的准确求解和余弦值的正负。解:(I) 证明:∵在直三棱柱
 中,
中,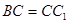 ,点
,点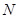 是
是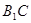 的中点,
的中点,∴
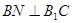 …………………………1分
…………………………1分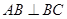 ,
, ,
,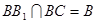
∴
 ⊥平面
⊥平面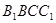 ………………………2分
………………………2分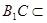 平面
平面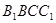
∴
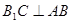 ,即
,即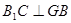 …………………3分
…………………3分又
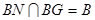
∴
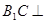 平面
平面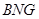 …………………………………4分
…………………………………4分(II)当
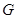 是棱
是棱 的中点时,
的中点时,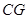 //平面
//平面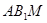 .……………………………5分
.……………………………5分证明如下:
 连结
连结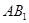 ,取
,取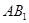 的中点H,连接
的中点H,连接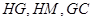 ,
, 则
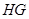 为
为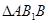 的中位线
的中位线 ∴
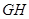 ∥
∥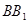 ,
,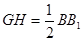 …………………6分
…………………6分∵由已知条件,
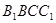 为正方形
为正方形∴
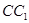 ∥
∥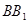 ,
,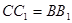
∵
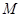 为
为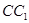 的中点,
的中点,∴
 ……………………7分
……………………7分∴
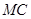 ∥
∥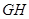 ,且
,且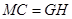
∴四边形
 为平行四边形
为平行四边形∴
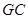 ∥
∥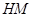
又 ∵

∴
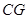 //平面
//平面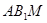 ……………………8分
……………………8分(III)∵直三棱柱
 且
且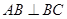
依题意,如图:以
 为原点建立空间直角坐标系
为原点建立空间直角坐标系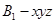 ,……………………9分
,……………………9分
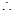
 ,
,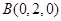 ,
,
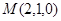
 ,
,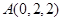 ,
,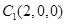
则
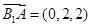 ,
,
设平面
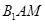 的法向量
的法向量 ,
, 则
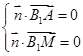 ,即
,即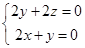 ,
,令
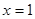 ,有
,有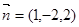 ……………………10分
……………………10分又
 平面
平面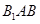 的法向量为
的法向量为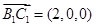 ,
,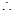
 =
= =
=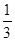 , ……………………11分
, ……………………11分设二面角
 的平面角为
的平面角为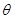 ,且
,且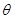 为锐角
为锐角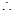
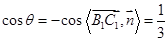 . ……………………12分.
. ……………………12分.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,
中,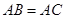 ,
,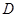 为
为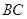 的中点,
的中点,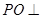 平面
平面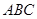 ,垂足
,垂足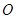 落在线段
落在线段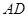 上,已知
上,已知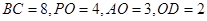 。
。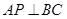 ;
;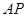 上是否存在点M,使得二面角
上是否存在点M,使得二面角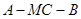 为直二面角?若存在,求
为直二面角?若存在,求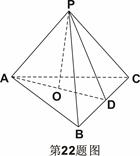
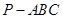 中,
中,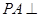 底面
底面 ,
,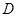 ,
,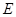 分别在棱
分别在棱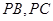 上,且
上,且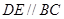
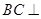 平面
平面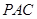 ;
;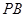 的中点时,求
的中点时,求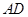 与平面
与平面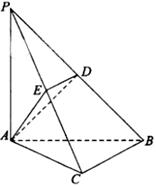
 中, AB=1,
中, AB=1, ,
, .
. ;
; —B的正切值。
—B的正切值。
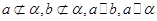 。求证:
。求证: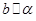 。
。
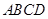 的对角线
的对角线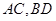 交于点
交于点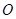 ,
,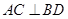 ,且
,且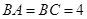 ,
,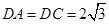 ,
,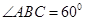 .现沿对角线
.现沿对角线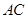 将三角形
将三角形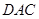 翻折,使得平面
翻折,使得平面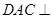 平面
平面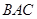 .翻折后: (Ⅰ)证明:
.翻折后: (Ⅰ)证明: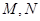 分别为
分别为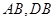 的中点.①求二面角
的中点.①求二面角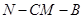 大小的余弦值; ②求点
大小的余弦值; ②求点 到平面
到平面 的距离
的距离 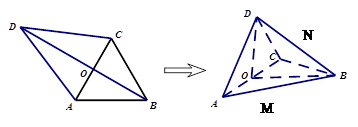
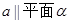 ,
, 那么过点P且平行于直线
那么过点P且平行于直线 的直线 ( )
的直线 ( ) 内
内