题目内容
如图 5,已知正方形ABCD在水平面上的正投影(投影线垂直于投影面)是四边形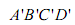 ,其中A与A '重合,且BB'<DD'<CC'.
,其中A与A '重合,且BB'<DD'<CC'.
(1)证明AD'//平面BB'C'C,并指出四边形AB'C'D’的形状;
(2)如果四边形中AB'C'D’中,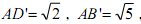 ,正方形的边长为
,正方形的边长为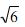 ,
,
求平面ABCD与平面AB'C'D’所成的锐二面角 的余弦值.
的余弦值.
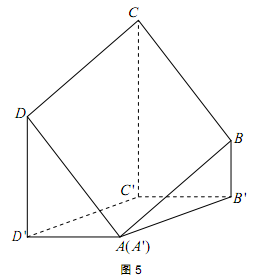
 ,其中A与A '重合,且BB'<DD'<CC'.
,其中A与A '重合,且BB'<DD'<CC'.(1)证明AD'//平面BB'C'C,并指出四边形AB'C'D’的形状;
(2)如果四边形中AB'C'D’中,
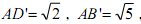 ,正方形的边长为
,正方形的边长为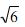 ,
,求平面ABCD与平面AB'C'D’所成的锐二面角
 的余弦值.
的余弦值.
见解析.
第一问是涉及到线面平行的判定,以及四边形的形状问题的证明。
第二问关于二面角的求解,可以利用射影面积公式法,也可以利用法向量的夹角公式来解,通过合理的建立直角坐标系,表示向量,然后求解斜率的夹角,利用互为补角的关系求解得到二面角的大小。
解:(2)依题意,在Rt△ABB’中, ,
,
在Rt△ADD’中, ,
,
所以 .………………8分
.………………8分

连结AC,AC’,如图5-2,在Rt△ACC’中, .
.
所以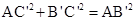 ,故
,故 .……10分
.……10分
(法1)延长CB,C’B’相交于点F,
则 ,所以
,所以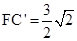 .
.
连结AF,则AF是平面ABCD与平面AB’C’D
的交线.
在平面AB’C’D
内作C’G,垂足为G,
连结 .
.
因为 平面AB’C’D,
平面AB’C’D,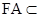 平面AB’C’D,所以
平面AB’C’D,所以 AF.
AF.
从而 平面CC’G,
平面CC’G,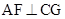 .
.
所以 是平面ABCD与平面AB’C’D所成的一个锐二面角. …………12分
是平面ABCD与平面AB’C’D所成的一个锐二面角. …………12分
在Rt△AC’F中, ,
,
在Rt△CC’G中,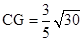 .
.
所以 ,
,
即平面ABCD与平面AB'C'D’所成的锐二面角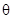 的余弦值为
的余弦值为 .………14分
.………14分

(法2)以c’为原点,c’a为x轴,c’b’为y轴,c’c为z轴,
建立空间直角坐标系(如图5-3),
则平面AB’C’D的一个法向量 .
.
设平面ABCD的一个法向量为 ,
,
因为

取z=1,则y= ,x=
,x= ,所以平面ABCD的一个法向量为
,所以平面ABCD的一个法向量为 .
.
(注:法向量不唯一,可以是与 共线的任一非零向量)……………12分
共线的任一非零向量)……………12分
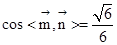 .
.
所以平面ABCD与平面AB’C’D所成的锐二面角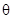 的余弦值为
的余弦值为 .…………………14分
.…………………14分
(法3)由题意,正方形ABCD在水平面上的正投影是四边形AB’C’D,
所以平面ABCD与平面AB’C’D,所成的锐二面角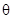 的余弦值
的余弦值 . …………12分
. …………12分
所以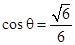 ,
,
所以平面ABCD与平面AB’C’D所成的锐二面角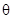 的余弦值为
的余弦值为 .…………………14分
.…………………14分
第二问关于二面角的求解,可以利用射影面积公式法,也可以利用法向量的夹角公式来解,通过合理的建立直角坐标系,表示向量,然后求解斜率的夹角,利用互为补角的关系求解得到二面角的大小。
解:(2)依题意,在Rt△ABB’中,
 ,
,在Rt△ADD’中,
 ,
,所以
 .………………8分
.………………8分
连结AC,AC’,如图5-2,在Rt△ACC’中,
 .
.所以
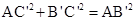 ,故
,故 .……10分
.……10分(法1)延长CB,C’B’相交于点F,
则
 ,所以
,所以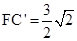 .
.连结AF,则AF是平面ABCD与平面AB’C’D
的交线.
在平面AB’C’D
内作C’G,垂足为G,
连结
 .
.因为
 平面AB’C’D,
平面AB’C’D,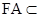 平面AB’C’D,所以
平面AB’C’D,所以 AF.
AF.从而
 平面CC’G,
平面CC’G,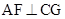 .
.所以
 是平面ABCD与平面AB’C’D所成的一个锐二面角. …………12分
是平面ABCD与平面AB’C’D所成的一个锐二面角. …………12分在Rt△AC’F中,
 ,
,在Rt△CC’G中,
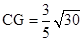 .
.所以
 ,
,即平面ABCD与平面AB'C'D’所成的锐二面角
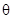 的余弦值为
的余弦值为 .………14分
.………14分
(法2)以c’为原点,c’a为x轴,c’b’为y轴,c’c为z轴,
建立空间直角坐标系(如图5-3),
则平面AB’C’D的一个法向量
 .
.设平面ABCD的一个法向量为
 ,
,因为

取z=1,则y=
 ,x=
,x= ,所以平面ABCD的一个法向量为
,所以平面ABCD的一个法向量为 .
.(注:法向量不唯一,可以是与
 共线的任一非零向量)……………12分
共线的任一非零向量)……………12分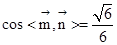 .
.所以平面ABCD与平面AB’C’D所成的锐二面角
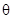 的余弦值为
的余弦值为 .…………………14分
.…………………14分(法3)由题意,正方形ABCD在水平面上的正投影是四边形AB’C’D,
所以平面ABCD与平面AB’C’D,所成的锐二面角
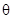 的余弦值
的余弦值 . …………12分
. …………12分所以
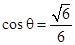 ,
,所以平面ABCD与平面AB’C’D所成的锐二面角
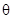 的余弦值为
的余弦值为 .…………………14分
.…………………14分
练习册系列答案
相关题目
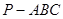 中,
中,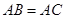 ,
,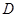 为
为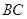 的中点,
的中点,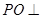 平面
平面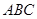 ,垂足
,垂足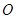 落在线段
落在线段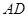 上,已知
上,已知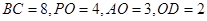 。
。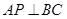 ;
;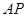 上是否存在点M,使得二面角
上是否存在点M,使得二面角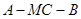 为直二面角?若存在,求
为直二面角?若存在,求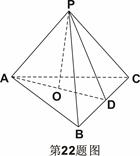
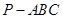 中,
中,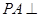 底面
底面 ,
,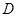 ,
,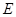 分别在棱
分别在棱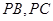 上,且
上,且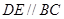
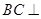 平面
平面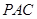 ;
;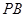 的中点时,求
的中点时,求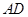 与平面
与平面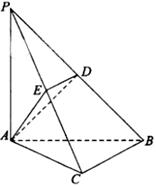
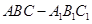 中, AB=1,
中, AB=1, ,
, .
. ;
; —B的正切值。
—B的正切值。
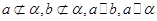 。求证:
。求证: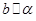 。
。 、
、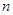 ,平面
,平面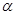 、
、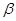 ,给出下列命题:
,给出下列命题: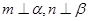 ,且
,且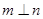 ,则
,则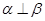 ②若
②若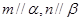 ,且
,且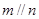 ,则
,则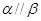
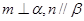 ,且
,且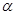 、
、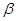 、
、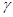 和直线
和直线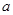 、
、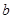 、
、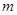 、
、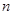 ,下列命题中真命题是( )
,下列命题中真命题是( )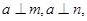
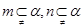 ,则
,则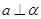 ;
;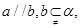 则
则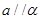 ;
;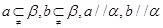 ,则
,则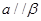 ;
;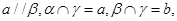 则
则 .
. 处,同一时刻,一个长
处,同一时刻,一个长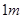 ,一端接触地面且与地面垂直的竹竿的影子长为
,一端接触地面且与地面垂直的竹竿的影子长为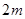 ,则该球的半径等于( )
,则该球的半径等于( )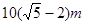

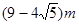
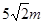
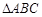 中,D,E,F分别是AB,AC和BC边的中点,
中,D,E,F分别是AB,AC和BC边的中点,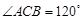 ,现将
,现将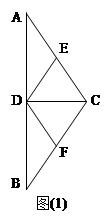
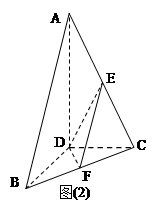
 DE?证明你的结论.
DE?证明你的结论.