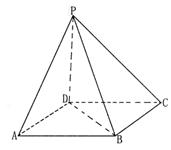
题目内容
如图所示,多面体FE-ABCD中,ABCD和ACFE都是直角梯形,DC∥AB,AE∥CF,平面ACFE⊥平面ABCD,AD=DC=CF=2AE=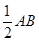 ,∠ACF=∠ADC=
,∠ACF=∠ADC=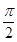 。
。
(I)求证:BC⊥平面ACFE;
(II)求二面角B-FE-D的平面角的余弦值。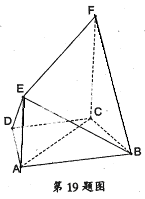
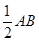 ,∠ACF=∠ADC=
,∠ACF=∠ADC=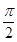 。
。(I)求证:BC⊥平面ACFE;
(II)求二面角B-FE-D的平面角的余弦值。

解:(Ⅰ)在直角梯形ABCD中,∵
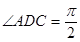 ,又AD=DC=
,又AD=DC=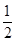 AB,可证BC⊥AC,
AB,可证BC⊥AC,………2分
又∵平面ACFE⊥平面ABCD,且平面ACFE∩平面ABCD=AC,
∴BC⊥平面ACFE;………4分
(Ⅱ)以A为原点,分别以AB、AD、AE为x,y,z轴,建立空间直角坐标系,
设AE=a,则D(0, 2a,0),B(4a,0 ,0),E(0,0,a),F(2a,2a,2a), ………6分
设
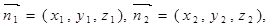
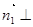 平面BEF,
平面BEF,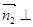 平面DEF,
平面DEF,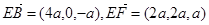 ,
,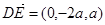
则
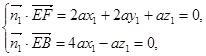
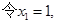
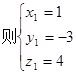 ,
,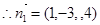
………8分
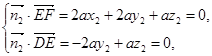
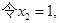
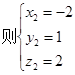 ,
,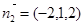
………9分
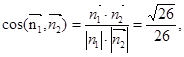
故所求二面角B-EF-D的平面角的余弦值是
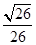 . ………12分
. ………12分略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 中,
中,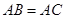 ,
,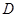 为
为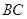 的中点,
的中点,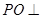 平面
平面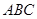 ,垂足
,垂足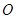 落在线段
落在线段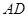 上,已知
上,已知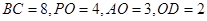 。
。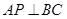 ;
;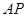 上是否存在点M,使得二面角
上是否存在点M,使得二面角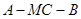 为直二面角?若存在,求
为直二面角?若存在,求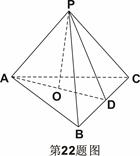
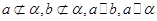 。求证:
。求证: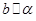 。
。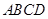 的对角线
的对角线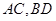 交于点
交于点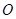 ,
,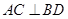 ,且
,且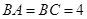 ,
,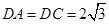 ,
,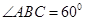 .现沿对角线
.现沿对角线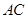 将三角形
将三角形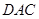 翻折,使得平面
翻折,使得平面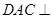 平面
平面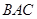 .翻折后: (Ⅰ)证明:
.翻折后: (Ⅰ)证明: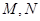 分别为
分别为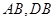 的中点.①求二面角
的中点.①求二面角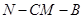 大小的余弦值; ②求点
大小的余弦值; ②求点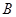 到平面
到平面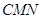 的距离
的距离 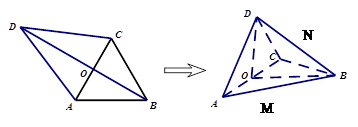
 A
A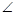 AOB和
AOB和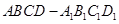 中,
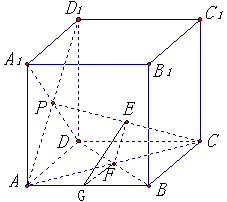
中,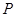 为侧面
为侧面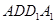 的中心,
的中心,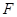 为底面
为底面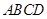 的中心,
的中心,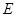 为
为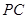 的中点,G为AB的 中点,
的中点,G为AB的 中点,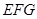 //平面
//平面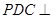 平面
平面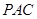 .
.
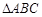 中,D,E,F分别是AB,AC和BC边的中点,
中,D,E,F分别是AB,AC和BC边的中点,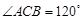 ,现将
,现将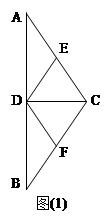
 DE?证明你的结论.
DE?证明你的结论.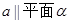 ,
,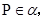 那么过点P且平行于直线
那么过点P且平行于直线 的直线 ( )
的直线 ( )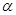 内
内