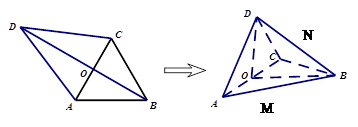
题目内容
已知平面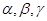 ,直线
,直线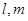 满足:
满足: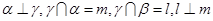 ,那么
,那么
①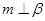 ; ②
; ②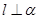 ; ③
; ③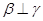 ; ④
; ④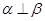 。
。
可由上述条件可推出的结论有 ;
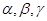 ,直线
,直线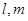 满足:
满足: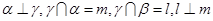 ,那么
,那么①
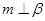 ; ②
; ②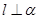 ; ③
; ③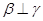 ; ④
; ④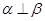 。
。可由上述条件可推出的结论有 ;
②④,
解:因为平面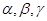 ,直线
,直线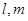 满足:
满足: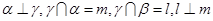
有两个平面同时与第三个平面垂直,并且交线垂直,则说明了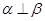 ,同时利用线面垂直的性质定理可知
,同时利用线面垂直的性质定理可知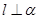 ,可推出的结论有②④,
,可推出的结论有②④,
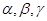 ,直线
,直线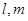 满足:
满足: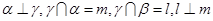
有两个平面同时与第三个平面垂直,并且交线垂直,则说明了
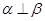 ,同时利用线面垂直的性质定理可知
,同时利用线面垂直的性质定理可知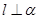 ,可推出的结论有②④,
,可推出的结论有②④,
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
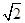 .
.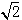 ,PD⊥BC。
,PD⊥BC。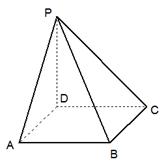
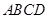 是等腰梯形,
是等腰梯形,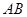 ∥
∥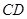 ,
,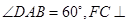 平面
平面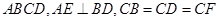 .
.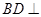 平面
平面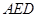 ;
;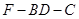 的余弦值.
的余弦值.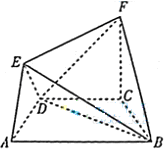
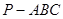 中,
中,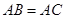 ,
,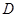 为
为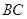 的中点,
的中点,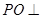 平面
平面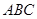 ,垂足
,垂足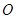 落在线段
落在线段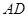 上,已知
上,已知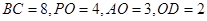 。
。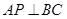 ;
;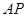 上是否存在点M,使得二面角
上是否存在点M,使得二面角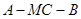 为直二面角?若存在,求
为直二面角?若存在,求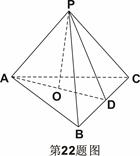
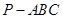 中,
中,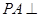 底面
底面 ,
,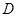 ,
,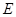 分别在棱
分别在棱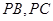 上,且
上,且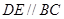
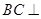 平面
平面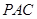 ;
;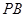 的中点时,求
的中点时,求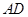 与平面
与平面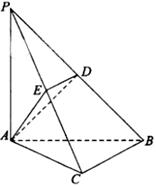
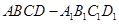 的底面边长为
的底面边长为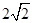 ,
,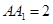 ,点
,点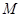 是
是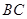 的中点,
的中点,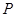 是平面
是平面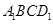 内的一个动点,且满足
内的一个动点,且满足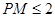 ,
,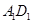 和
和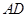 的距离相等,则点
的距离相等,则点
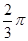
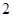
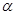 、
、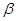 、
、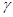 和直线
和直线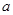 、
、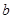 、
、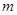 、
、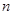 ,下列命题中真命题是( )
,下列命题中真命题是( )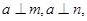
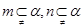 ,则
,则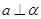 ;
;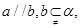 则
则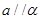 ;
;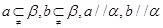 ,则
,则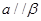 ;
;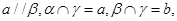 则
则 .
.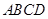 的对角线
的对角线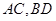 交于点
交于点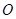 ,
,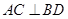 ,且
,且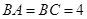 ,
,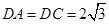 ,
,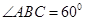 .现沿对角线
.现沿对角线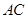 将三角形
将三角形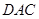 翻折,使得平面
翻折,使得平面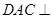 平面
平面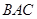 .翻折后: (Ⅰ)证明:
.翻折后: (Ⅰ)证明: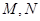 分别为
分别为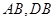 的中点.①求二面角
的中点.①求二面角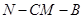 大小的余弦值; ②求点
大小的余弦值; ②求点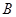 到平面
到平面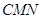 的距离
的距离