题目内容
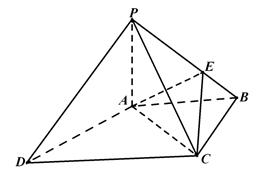
(12分)已知四棱锥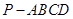 的底面为直角梯形,
的底面为直角梯形,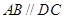 ,
,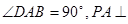 底面
底面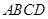 ,且
,且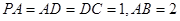 ,
,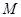 是
是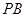 的中点.
的中点.
(Ⅰ)证明:面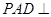 面
面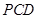 ;
;
(Ⅱ)求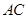 与
与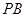 所成的角余弦值;
所成的角余弦值;
(Ⅲ)求面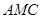 与面
与面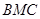 所成二面角的余弦值.
所成二面角的余弦值.
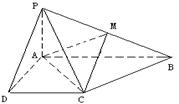
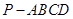 的底面为直角梯形,
的底面为直角梯形,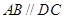 ,
,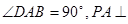 底面
底面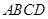 ,且
,且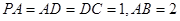 ,
,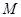 是
是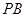 的中点.
的中点.(Ⅰ)证明:面
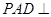 面
面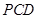 ;
;(Ⅱ)求
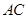 与
与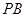 所成的角余弦值;
所成的角余弦值;(Ⅲ)求面
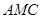 与面
与面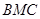 所成二面角的余弦值.
所成二面角的余弦值.
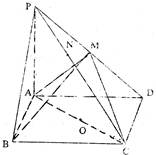
证明:以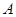 为坐标原点
为坐标原点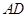 长为单位长度,如图建立空间直角坐标系,则各点坐标为
长为单位长度,如图建立空间直角坐标系,则各点坐标为
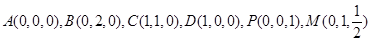 .
.
(Ⅰ)证明:因
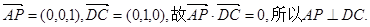
由题设知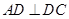 ,且
,且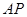 与
与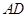 是平面
是平面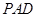 内的两条相交直线,由此得
内的两条相交直线,由此得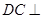 面
面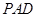 .又
.又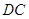 在面
在面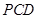 上,故面
上,故面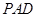 ⊥面
⊥面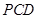 . …………………… 3分
. …………………… 3分
(Ⅱ)解:因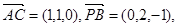
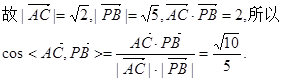 ……… 6分
……… 6分
(Ⅲ)解:在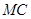 上取一点
上取一点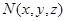 ,则存在
,则存在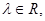 使
使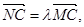
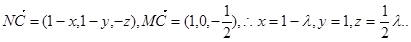
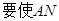
 MC,只需
MC,只需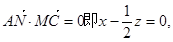 解得
解得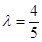
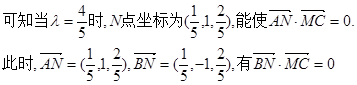
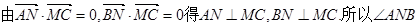 为所求二面角的平面角.
为所求二面角的平面角.

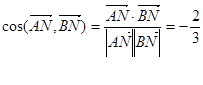
所以二面角的余弦值为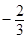 ……… 12分
……… 12分
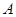 为坐标原点
为坐标原点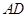 长为单位长度,如图建立空间直角坐标系,则各点坐标为
长为单位长度,如图建立空间直角坐标系,则各点坐标为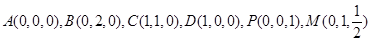 .
.(Ⅰ)证明:因
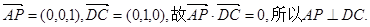
由题设知
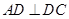 ,且
,且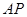 与
与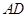 是平面
是平面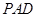 内的两条相交直线,由此得
内的两条相交直线,由此得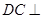 面
面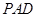 .又
.又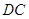 在面
在面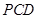 上,故面
上,故面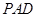 ⊥面
⊥面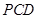 . …………………… 3分
. …………………… 3分 (Ⅱ)解:因
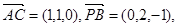
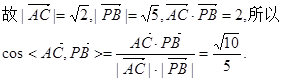 ……… 6分
……… 6分(Ⅲ)解:在
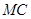 上取一点
上取一点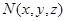 ,则存在
,则存在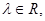 使
使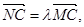
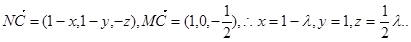
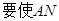
 MC,只需
MC,只需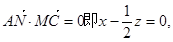 解得
解得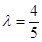
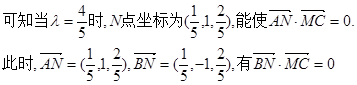
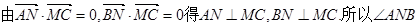 为所求二面角的平面角.
为所求二面角的平面角.
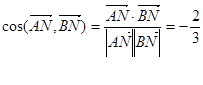
所以二面角的余弦值为
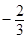 ……… 12分
……… 12分略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
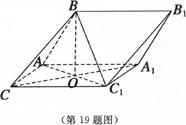
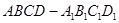 中,E、F分别是中点。
中,E、F分别是中点。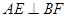 ;
;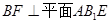 ;
;
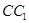 上是否存在点P使
上是否存在点P使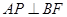 ,若存在,确定点P位置;若不存在,说明理由。
,若存在,确定点P位置;若不存在,说明理由。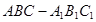 中,
中,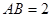 ,
,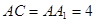 ,
,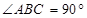 .
.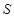 ;
;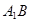 与
与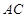 所成角的大小(结果用反三角函数表示).
所成角的大小(结果用反三角函数表示).
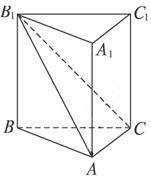
 ,则下列推论中正确的是( )
,则下列推论中正确的是( ) ,则
,则
 ,b//
,b// 共面,则
共面,则
 ,则a//b
,则a//b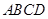 中,
中,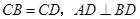 ,点
,点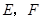 分别是
分别是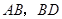 的中点. 求证:
的中点. 求证: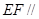 平面
平面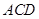 ;
;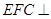 平面
平面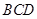 .
.
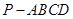 中,
中,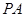 ⊥底面
⊥底面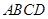 ,底面
,底面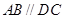 ,
,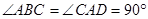 ,且
,且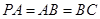 ,点
,点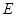 是棱
是棱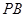 上的动点.
上的动点.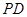 ∥平面
∥平面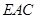 时,确定点
时,确定点 棱
棱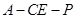 的余弦值.
的余弦值.