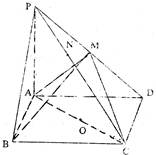
题目内容
在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=A,AB=2,以AC的中点O为球心、AC为直径的球面交PD于点M。
(1)求证:平面ABM⊥平面PCD;
(2)求直线CD与平面ACM所成的角的大小;
(1)求证:平面ABM⊥平面PCD;
(2)求直线CD与平面ACM所成的角的大小;

(1)依题设知,AC是所作球面的直径,则AM⊥MC。
又因为PA⊥平面ABCD,则PA⊥CD,又CD⊥AD,
所以CD⊥平面PAD,则CD⊥AM,所以AM⊥平面PCD,
所以平面ABM⊥平面PCD。
(2)如图所示,建立空间直角坐标系,则A(0,0,0),P(0,0,4),

B(2,0,0),C(2,4,0),D(0,4,0),M(0,2,2);
设平面ACM的一个法向量

所以所求角的大小为arcsin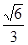 。
。
又因为PA⊥平面ABCD,则PA⊥CD,又CD⊥AD,
所以CD⊥平面PAD,则CD⊥AM,所以AM⊥平面PCD,
所以平面ABM⊥平面PCD。
(2)如图所示,建立空间直角坐标系,则A(0,0,0),P(0,0,4),

B(2,0,0),C(2,4,0),D(0,4,0),M(0,2,2);
设平面ACM的一个法向量

所以所求角的大小为arcsin
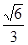 。
。略

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
 的底面为直角梯形,
的底面为直角梯形,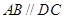 ,
,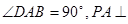 底面
底面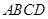 ,且
,且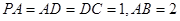 ,
,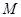 是
是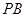 的中点.
的中点.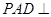 面
面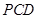 ;
;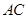 与
与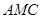 与面
与面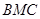 所成二面角的余弦值.
所成二面角的余弦值.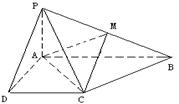
 ACB=90°,AC=BC=AA1=1,D、E分别为棱AB、
ACB=90°,AC=BC=AA1=1,D、E分别为棱AB、 BC的中点,M为棱AA1上的点。
BC的中点,M为棱AA1上的点。 的大小。
的大小。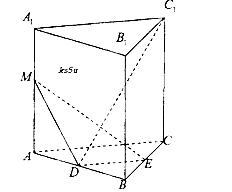
 β
β 中,
中, 分别为
分别为
 的中点.
的中点. 平面
平面 ;
; 的正切值.
的正切值.
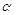 、
、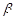 为不同的平面,则正确的命题是
为不同的平面,则正确的命题是 ,则 l⊥
,则 l⊥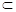 β,则下面四个命题:
β,则下面四个命题:
 不共面的射线
不共面的射线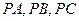 两两之间的夹角都是
两两之间的夹角都是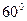 ,则平面
,则平面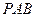 与平面
与平面 所成的
所成的