题目内容
【题目】在一段时间内，分5次测得某种商品的价格x(万元)和需求量y(t)之间的一组数据为：
1 | 2 | 3 | 4 | 5 | |
价格x | 1.4 | 1.6 | 1.8 | 2 | 2.2 |
需求量y | 12 | 10 | 7 | 5 | 3 |
已知
，
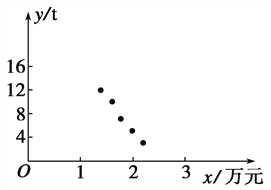
(1)画出散点图；
(2)求出y对x的线性回归方程；
(3)如价格定为1.9万元，预测需求量大约是多少？(精确到0.01 t)．
参考公式：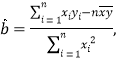
.
【答案】(1)见解析；（2）y＝28.1－11.5x;(3)6.25t.
【解析】分析：（1）先描出各点即得散点图.(2)利用最小二乘法求出y对x的线性回归方程.(3)令x=1.9即得需求量.
详解：(1)散点图如图所示：
(2)因为
×9＝1.8，
×37＝7.4，
，
所以
＝
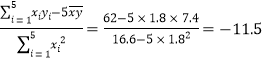
a=
－ b
＝7.4＋11.5×1.8＝28.1，
故y对x的线性回归方程为 y＝28.1－11.5x.
(3)当x=1.9时，y ＝28.1－11.5×1.9＝6.25(t)，
所以如价格定为1.9万元，预测需求量大约是6.25(t).
练习册系列答案
相关题目
【题目】甲、乙两同学5次综合测评的成绩如茎叶图所示．
甲 | 乙 | |||||
9 | 8 | 8 | 3 | 3 | 7 | |
2 | 1 | 0 | 9 | ● | 9 |
老师在计算甲、乙两人平均分时，发现乙同学成绩的一个数字无法看清．若从{0，1，2，…，9}随机取一个数字代替，则乙的平均成绩超过甲的平均成绩的概率为（ ）
A.
B.
C.
D.
