题目内容
【题目】设函数f(x)=ax2+lnx.
(Ⅰ)当a=﹣1时,求函数y=f(x)的图象在点(1,f(1))处的切线方程;
(Ⅱ)已知a<0,若函数y=f(x)的图象总在直线y=-![]() 的下方,求a的取值范围;
的下方,求a的取值范围;
(Ⅲ)记f′(x)为函数f(x)的导函数.若a=1,试问:在区间[1,10]上是否存在k(k<100)个正数x1 , x2 , x3…xk , 使得f′(x1)+f′(x2)+f′(x3)+…+f′(xk)≥2012成立?请证明你的结论.
【答案】解:(Ⅰ)当a=﹣1时,f(x)=﹣x2+lnx,![]() ,f′(1)=﹣1,
,f′(1)=﹣1,
所以切线的斜率为﹣1.
又f(1)=﹣1,所以切点为(1,﹣1).
故所求的切线方程为:y+1=﹣(x﹣1)即x+y=0.
(Ⅱ)![]() ,x>0,a<0.
,x>0,a<0.
令f′(x)=0,则x=![]() .
.
当x![]() (0,
(0,![]() )时,f′(x)>0;当x
)时,f′(x)>0;当x![]() (
(![]() ,+
,+![]() )时,f′(x)<0.
)时,f′(x)<0.
故x=![]() 为函数f(x)的唯一极大值点,
为函数f(x)的唯一极大值点,
所以f(x)的最大值为f(![]() )=-
)=-![]() .
.
由题意有![]()
![]() ,解得a
,解得a![]() .
.
所以a的取值范围为(-![]() ,-
,-![]() )
)
(Ⅲ)当a=1时,![]() .记g(x)=f′(x),其中x∈[1,10].
.记g(x)=f′(x),其中x∈[1,10].
∵当x∈[1,10]时,![]() ,∴y=g(x)在[1,10]上为增函数,
,∴y=g(x)在[1,10]上为增函数,
即y=f′(x)在[1,10]上为增函数
又![]() ,
,
所以,对任意的x∈[1,10],总有![]() .
.
所以f'(x1)+f'(x2)+f'(x3)+…+f'(xk)≤![]() ,
,
又因为k<100,所以![]() .
.
故在区间[1,10]上不存在使得f'(x1)+f'(x2)+f'(x3)+…+f'(xk)≥2012成立的k(k<100)个正数x1 , x2 , x3…xk .
【解析】(Ⅰ)当a=﹣1时,![]() , f′(1)=﹣1,由此能求出函数y=f(x)的图象在点(1,f(1))处的切线方程.
, f′(1)=﹣1,由此能求出函数y=f(x)的图象在点(1,f(1))处的切线方程.
(Ⅱ)![]() , x>0,a<0.令f′(x)=0,则x=
, x>0,a<0.令f′(x)=0,则x=![]() . 由此能求出a的取值范围.
. 由此能求出a的取值范围.
(Ⅲ)当a=1时,![]() . 记g(x)=f′(x),其中x∈[1,10].由此入手能够推导出在区间[1,10]上不存在使得f'(x1)+f'(x2)+f'(x3)+…+f'(xk)≥2012成立的k(k<100)个正数x1 , x2 , x3…xk .
. 记g(x)=f′(x),其中x∈[1,10].由此入手能够推导出在区间[1,10]上不存在使得f'(x1)+f'(x2)+f'(x3)+…+f'(xk)≥2012成立的k(k<100)个正数x1 , x2 , x3…xk .

 阅读快车系列答案
阅读快车系列答案【题目】在一段时间内,分5次测得某种商品的价格x(万元)和需求量y(t)之间的一组数据为:
1 | 2 | 3 | 4 | 5 | |
价格x | 1.4 | 1.6 | 1.8 | 2 | 2.2 |
需求量y | 12 | 10 | 7 | 5 | 3 |
已知![]() ,
,
(1)画出散点图;
(2)求出y对x的线性回归方程;
(3)如价格定为1.9万元,预测需求量大约是多少?(精确到0.01 t).
参考公式: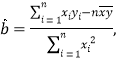
![]() .
.
【题目】某学校为调查高三年学生的身高情况,按随机抽样的方法抽取80名学生,得到男生身高情况的频率分布直方图(图(1))和女生身高情况的频率分布直方图(图(2)).已知图(1)中身高在170~175cm的男生人数有16人.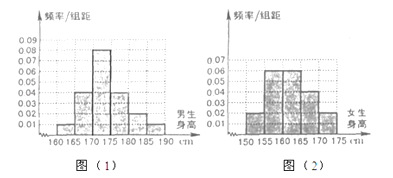
(Ⅰ)试问在抽取的学生中,男、女生各有多少人?
(Ⅱ)根据频率分布直方图,完成下列的2×2列联表,并判断能有多大(百分几)的把握认为“身高与性别有关”?
≥170cm | <170cm | 总计 | |
男生身高 | |||
女生身高 | |||
总计 |
(Ⅲ)在上述80名学生中,从身高在170~175cm之间的学生中按男、女性别分层抽样的方法,抽出5人,从这5人中选派3人当旗手,求3人中恰好有一名女生的概率.
参考公式:K2=![]()
参考数据:
P(K2≥k0) | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费![]() (单位:万元)对年销售量
(单位:万元)对年销售量![]() (单位:吨)和年利润
(单位:吨)和年利润![]() (单位:万元)的影响.对近六年的年宣传费
(单位:万元)的影响.对近六年的年宣传费![]() 和年销售量
和年销售量![]() 的数据作了初步统计,得到如下数据:
的数据作了初步统计,得到如下数据:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
年宣传费 | 38 | 48 | 58 | 68 | 78 | 88 |
年销售量 | 16.8 | 18.8 | 20.7 | 22.4 | 24.0 | 25.5 |
经电脑模拟,发现年宣传费![]() (万元)与年销售量
(万元)与年销售量![]() (吨)之间近似满足关系式
(吨)之间近似满足关系式![]() ,即
,即![]() .对上述数据作了初步处理,得到相关的值如下表:
.对上述数据作了初步处理,得到相关的值如下表:
|
|
|
|
75.3 | 24.6 | 18.3 | 101.4 |
(1)根据所给数据,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)规定当产品的年销售量![]() (吨)与年宣传费
(吨)与年宣传费![]() (万元)的比值在区间
(万元)的比值在区间![]() 内时认为该年效益良好.该公司某
内时认为该年效益良好.该公司某![]() 年投入的宣传费用(单位:万元)分别为:
年投入的宣传费用(单位:万元)分别为:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,试根据回归方程估计年销售量,从这
,试根据回归方程估计年销售量,从这![]() 年中任选
年中任选![]() 年,记其中选到效益良好年的数量为
年,记其中选到效益良好年的数量为![]() ,试求随机变量
,试求随机变量![]() 的分布列和期望.(其中
的分布列和期望.(其中![]() 为自然对数的底数,
为自然对数的底数,![]() )
)
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 中的斜率和截距的最小二乘估计分别为
中的斜率和截距的最小二乘估计分别为 ,
,![]() .
.
