题目内容
【题目】设 ![]() ,
, ![]() ,
, ![]() 是非零向量,已知命题p:若
是非零向量,已知命题p:若 ![]()
![]() =0,
=0, ![]()
![]() =0,则
=0,则 ![]()
![]() =0;命题q:若
=0;命题q:若 ![]() ∥
∥ ![]() ,
, ![]() ∥
∥ ![]() ,则
,则 ![]() ∥
∥ ![]() ,则下列命题中真命题是( )
,则下列命题中真命题是( )
A.p∨q
B.p∧q
C.(¬p)∧(¬q)
D.p∨(¬q)
【答案】A
【解析】解:若 ![]()
![]() =0,
=0, ![]()
![]() =0,则
=0,则 ![]()
![]() =
= ![]()
![]() ,即(
,即( ![]() ﹣
﹣ ![]() )
) ![]() =0,则
=0,则 ![]()
![]() =0不一定成立,故命题p为假命题,
=0不一定成立,故命题p为假命题,
若 ![]() ∥
∥ ![]() ,
, ![]() ∥
∥ ![]() ,则
,则 ![]() ∥
∥ ![]() 平行,故命题q为真命题,
平行,故命题q为真命题,
则p∨q,为真命题,p∧q,(¬p)∧(¬q),p∨(¬q)都为假命题,
故选:A.
【考点精析】认真审题,首先需要了解复合命题的真假(“或”、 “且”、 “非”的真值判断:“非p”形式复合命题的真假与F的真假相反;“p且q”形式复合命题当P与q同为真时为真,其他情况时为假;“p或q”形式复合命题当p与q同为假时为假,其他情况时为真).

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
【题目】在一段时间内,分5次测得某种商品的价格x(万元)和需求量y(t)之间的一组数据为:
1 | 2 | 3 | 4 | 5 | |
价格x | 1.4 | 1.6 | 1.8 | 2 | 2.2 |
需求量y | 12 | 10 | 7 | 5 | 3 |
已知![]() ,
,
(1)画出散点图;
(2)求出y对x的线性回归方程;
(3)如价格定为1.9万元,预测需求量大约是多少?(精确到0.01 t).
参考公式: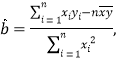
![]() .
.