题目内容
【题目】已知向量![]() =(sin(A-B),2cosA)
=(sin(A-B),2cosA)![]() =(1,cos(
=(1,cos(![]() -B)),且
-B)),且![]()
![]()
![]() =-sin2C,其中A、B、C分别为△ABC的三边a、b、c所对的角.
=-sin2C,其中A、B、C分别为△ABC的三边a、b、c所对的角.
(Ⅰ)求角C的大小;
(Ⅱ)若sinA+sinB=![]() sinC,且
sinC,且![]() , 求c.
, 求c.
【答案】解:(Ⅰ)∵![]() =(sin(A﹣B),2cosA),
=(sin(A﹣B),2cosA),![]() =(1,cos(
=(1,cos(![]() ﹣B)),
﹣B)),
∴![]()
![]() =sin(A﹣B)+2cosAcos(
=sin(A﹣B)+2cosAcos(![]() ﹣B)=sin(A+B),
﹣B)=sin(A+B),
又∵![]()
![]() =﹣2sin2C,
=﹣2sin2C,
∴sin(A+B)=﹣sin2C,
∵sin(A+B)=sinC,
∴sinC=﹣sin2C=﹣2sinCcosC,
∵0<C<π,
∴sinC≠0,
∴cosC=﹣![]() ,
,
又∵0<C<π,
∴C=![]() ;
;
(Ⅱ)∵sinA+sinB=![]() sinC,由正弦定理得a+b=
sinC,由正弦定理得a+b=![]() c,(1);
c,(1);
S△ABC=![]() absinC=
absinC=![]() ab
ab![]() =4
=4![]() ,得ab=16,(2)
,得ab=16,(2)
由余弦定理c2=a2+b2﹣2abcosC,得c2=a2+b2+ab,(3)
由(1)(2)(3)可得c=4![]() .
.
【解析】(Ⅰ)A、B、C为△ABC的内角,利用向量数量积的坐标运算可求得![]()
![]()
![]() =sin(A+B),与已知
=sin(A+B),与已知![]()
![]()
![]() =﹣2sin2C联立,即可求得角C的大小;
=﹣2sin2C联立,即可求得角C的大小;
(Ⅱ)利用正弦定理知,a+b=![]() c;由S△ABC=
c;由S△ABC=![]() absinC=4
absinC=4![]() 可得ab=16,再由余弦定理c2=a2+b2﹣2abcosC即可求得c的值.
可得ab=16,再由余弦定理c2=a2+b2﹣2abcosC即可求得c的值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】在一段时间内,分5次测得某种商品的价格x(万元)和需求量y(t)之间的一组数据为:
1 | 2 | 3 | 4 | 5 | |
价格x | 1.4 | 1.6 | 1.8 | 2 | 2.2 |
需求量y | 12 | 10 | 7 | 5 | 3 |
已知![]() ,
,
(1)画出散点图;
(2)求出y对x的线性回归方程;
(3)如价格定为1.9万元,预测需求量大约是多少?(精确到0.01 t).
参考公式: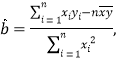
![]() .
.