题目内容
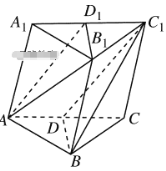
【题目】如图所示,在斜三棱柱ABC—A1B1C1中,点D,D1分别为AC,A1C1上的点.
(1)当![]() 的值等于何值时,BC1∥平面AB1D1;
的值等于何值时,BC1∥平面AB1D1;
(2)若平面BC1D∥平面AB1D1,求![]() 的值.
的值.
【答案】(1)1; (2)1.
【解析】
(1)取![]() 为线段
为线段![]() 的中点,此时
的中点,此时![]() =1,连接
=1,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,在
,在![]() 中,点
中,点![]() 分别为
分别为![]() 的中点,得
的中点,得![]() ,进而证得
,进而证得![]() 面
面![]() .
.
(2)由已知,平面![]() 平面
平面![]() ,进而得到
,进而得到![]() 和
和![]() ,进而可求解.
,进而可求解.
(1)如图所示,取D1为线段A1C1的中点,
此时![]() =1,连接A1B交AB1于点O,连接OD1.
=1,连接A1B交AB1于点O,连接OD1.
由棱柱的性质,知四边形A1ABB1为平行四边形,所以点O为A1B的中点.
在△A1BC1中,点O,D1分别为A1B,A1C1的中点,∴OD1∥BC1.
又∵OD1平面AB1D1,BC1平面AB1D1,
∴BC1∥平面AB1D1.∴![]() 时,BC1∥平面AB1D1.
时,BC1∥平面AB1D1.
(2)由已知,平面BC1D∥平面AB1D1,且平面A1BC1∩平面BDC1=BC1,
平面A1BC1∩平面AB1D1=D1O,因此BC1∥D1O,同理AD1∥DC1.
∴![]() .又∵
.又∵![]() ,∴
,∴![]() ,即
,即![]() .
.

练习册系列答案
相关题目
【题目】在一段时间内,分5次测得某种商品的价格x(万元)和需求量y(t)之间的一组数据为:
1 | 2 | 3 | 4 | 5 | |
价格x | 1.4 | 1.6 | 1.8 | 2 | 2.2 |
需求量y | 12 | 10 | 7 | 5 | 3 |
已知![]() ,
,
(1)画出散点图;
(2)求出y对x的线性回归方程;
(3)如价格定为1.9万元,预测需求量大约是多少?(精确到0.01 t).
参考公式: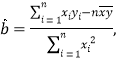
![]() .
.
