题目内容
已知函数f(x)=
cos2x+2sinx•sin(x+
)．
（Ⅰ）求f（x）的最小正周期，最大值以及取得最大值时x的集合；
（Ⅱ）若A是锐角△ABC的内角，f（A）=0，b=5，a=7，求△ABC的面积．
| 3 |
| π |
| 2 |
（Ⅰ）求f（x）的最小正周期，最大值以及取得最大值时x的集合；
（Ⅱ）若A是锐角△ABC的内角，f（A）=0，b=5，a=7，求△ABC的面积．
（Ⅰ）∵f(x)=
cos2x+2sinx•sin(x+
)=
cos2x+2sinx•cosx
=
cos2x+sin2x=2sin(2x+
)，…（4分）
∴f（x）的最小正周期是π．…（5分）
令 2x+
=
+2kπ，k∈Z，解得 x=
+kπ，k∈Z，
∴函数f（x）的最大值为2，此时，x值的集合为 {x|x=kπ+
，k∈z}．…（7分）
（Ⅱ）∵f(A)=sin(2A+
)=0，0＜A＜
∴A=
．…（9分）
在△ABC中，a2=b2+c2-2bc．cosA，c2-5c-24=0，解得c=8，或c=-3（舍），…（11分）
∴S△ABC=
bc•sinA=10
．…（13分）
| 3 |
| π |
| 2 |
| 3 |
=
| 3 |
| π |
| 3 |
∴f（x）的最小正周期是π．…（5分）
令 2x+
| π |
| 3 |
| π |
| 2 |
| π |
| 12 |
∴函数f（x）的最大值为2，此时，x值的集合为 {x|x=kπ+
| π |
| 12 |
（Ⅱ）∵f(A)=sin(2A+
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
在△ABC中，a2=b2+c2-2bc．cosA，c2-5c-24=0，解得c=8，或c=-3（舍），…（11分）
∴S△ABC=
| 1 |
| 2 |
| 3 |
练习册系列答案
相关题目
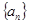（ n∈N*）中a1>1,公比q>0，设bn=log2an,且b1+b3+b5=6,b1·b3·b5=0.
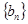是等差数列；