题目内容
在△ABC中,角A,B,C所对的边分别是a,b,c.己知csinA=
acosC.
(Ⅰ)求C;
(Ⅱ)若c=
,且sinC+sin(B-A)=3sin2A,求△ABC的面积.
| 3 |
(Ⅰ)求C;
(Ⅱ)若c=
| 7 |
(Ⅰ)∵csinA=
acosC,∴由正弦定理,得sinCsinA=
sinAcosC
结合sinA>0,可得sinC=
cosC,得tanC=
∵C是三角形的内角,∴C=60°;
(Ⅱ)∵sinC+sin(B-A)=sin(B+A)+sin(B-A)=2sinBcosA,
而3sin2A=6sinAcosA
∴由sinC+sin(B-A)=3sin2A,得sinBcosA=3sinAcosA
当cosA=0时,∠A=
,可得b=
=
,
可得三角△ABC的面积S=
bc=
当cosA≠0时,得sinB=3sinA,由正弦定理得b=3a…①,
∵c=
,∠C=60°,c2=a2+b2-2abcosC
∴a2+b2-ab=7…②,
联解①①得a=1,b=3,
∴△ABC的面积S=
absinC=
×1×3×sin60°=
.
综上所述,△ABC的面积等于
或
.
| 3 |
| 3 |
结合sinA>0,可得sinC=
| 3 |
| 3 |
∵C是三角形的内角,∴C=60°;
(Ⅱ)∵sinC+sin(B-A)=sin(B+A)+sin(B-A)=2sinBcosA,
而3sin2A=6sinAcosA
∴由sinC+sin(B-A)=3sin2A,得sinBcosA=3sinAcosA
当cosA=0时,∠A=
| π |
| 2 |
| c |
| tanC |
| ||
| 3 |
可得三角△ABC的面积S=
| 1 |
| 2 |
7
| ||
| 6 |
当cosA≠0时,得sinB=3sinA,由正弦定理得b=3a…①,
∵c=
| 7 |
∴a2+b2-ab=7…②,
联解①①得a=1,b=3,
∴△ABC的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
3
| ||
| 4 |
综上所述,△ABC的面积等于
7
| ||
| 6 |
3
| ||
| 4 |

练习册系列答案
 能力评价系列答案
能力评价系列答案
相关题目
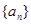 满足:
满足: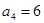 ,
,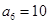 .
.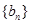 的各项均为正数,
的各项均为正数,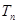 为其前
为其前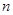 项和,若
项和,若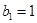 ,
,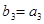 ,求
,求