题目内容
在△ABC中,角A、B、C的对边分别为a、b、c,设S为△ABC的面积,满足4S=
(a2+b2-c2).
(Ⅰ)求角C的大小;
(Ⅱ)若1+
=
,且
•
=-8,求c的值.
| 3 |
(Ⅰ)求角C的大小;
(Ⅱ)若1+
| tanA |
| tanB |
| 2c |
| b |
| AB |
| BC |
(Ⅰ)∵根据余弦定理得a2+b2-c2=2abcosC,△ABC的面积S=
absinC,
∴由4S=
(a2+b2-c2)得4×
absinC=2
abcosC,
化简得sinC=
cosC,可得tanC=
=
,
∵0<C<π,∴C=
;
(Ⅱ)∵1+
=
,∴1+
=
=
,
可得
=
,即
=
.
∴由正弦定理得
=
,解得cosA=
,结合0<A<π,得A=
.
∵△ABC中,C=
,∴B=π-(A+B)=
,
因此,
•
=-
•
=-|
|•|
|cosB=-
c2
∵
•
=-8,
∴-
c2=-8,解之得c=4(舍负).
| 1 |
| 2 |
∴由4S=
| 3 |
| 1 |
| 2 |
| 3 |
化简得sinC=
| 3 |
| sinC |
| cosC |
| 3 |
∵0<C<π,∴C=
| π |
| 3 |
(Ⅱ)∵1+
| tanA |
| tanB |
| 2c |
| b |
| sinAcosB |
| sinBcosA |
| cosAsinB+sinAcosB |
| cosAsinB |
| 2c |
| b |
可得
| sin(A+B) |
| cosAsinB |
| 2c |
| b |
| sinC |
| cosAsinB |
| 2c |
| b |
∴由正弦定理得
| sinC |
| cosAsinB |
| 2sinC |
| sinB |
| 1 |
| 2 |
| π |
| 3 |
∵△ABC中,C=
| π |
| 3 |
| π |
| 3 |
因此,
| AB |
| BC |
| BA |
| BC |
| BA |
| BC |
| 1 |
| 2 |
∵
| AB |
| BC |
∴-
| 1 |
| 2 |

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
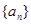 满足:
满足: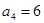 ,
,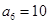 .
.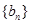 的各项均为正数,
的各项均为正数,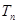 为其前
为其前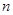 项和,若
项和,若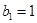 ,
,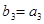 ,求
,求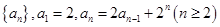
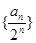 为等差数列;
为等差数列;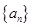 的前n项和
的前n项和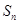 ;
;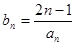 ,求数列
,求数列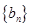 中的最大值.
中的最大值.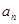 }中,
}中,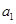 ="13" ,且前
="13" ,且前 项的算术平均数等于第
项的算术平均数等于第