题目内容
在△ABC中,角A、B、C所对的边分别为a,b,c,若b2+c2-a2=
bc,且b=
a,则下列关系一定不成立的是( )
| 3 |
| 3 |
| A.a=c | B.b=c | C.2a=c | D.a2+b2=c2 |
∵b2+c2-a2=
bc,
∴cosA=
=
,
∴A=30°,
由正弦定理化简b=
a,得到sinB=
sinA=
,
∴B=60°或120°,
当B=60°时,C=90°,此时△ABC为直角三角形,
得到a2+b2=c2,2a=c;
当B=120°时,C=30°,此时△ABC为等腰三角形,
得到a=c,
综上,b=c不一定成立,
故选:B.
| 3 |
∴cosA=
| b2+c2-a2 |
| 2bc |
| ||
| 2 |
∴A=30°,
由正弦定理化简b=
| 3 |
| 3 |
| ||
| 2 |
∴B=60°或120°,
当B=60°时,C=90°,此时△ABC为直角三角形,
得到a2+b2=c2,2a=c;
当B=120°时,C=30°,此时△ABC为等腰三角形,
得到a=c,
综上,b=c不一定成立,
故选:B.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
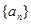 满足:
满足: ,
,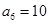 .
.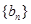 的各项均为正数,
的各项均为正数,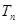 为其前
为其前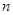 项和,若
项和,若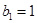 ,
,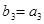 ,求
,求 的前
的前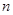 项和为
项和为 ,且
,且 ,数列
,数列 中,
中,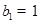 ,点
,点 在直线
在直线 上.
上.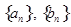 的通项
的通项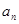 和
和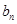 ;
; ,求数列
,求数列 的前n项和
的前n项和 .
.