题目内容

已知△ABC的内角A、B、C的对边分别为a、b、c，
3
sinCcosC-cos2C=
1
2
，且c=3．
（1）求角C；
（2）若向量
m
=(1，sinA)与
n
=(2，sinB)共线，求a、b的值．
（1）∵
3
sinCcosC-cos2C=
1
2
，
∴
3
2
sin2C-
1+cos2C
2
=
1
2

∴sin（2C-30°）=1
∵0°＜C＜180°
∴C=60°
（2）由（1）可得A+B=120°
∵
m
=(1，sinA)与
n
=(2，sinB)共线，
∴sinB-2sinA=0
∴sin（120°-A）=2sinA
整理可得，cosA=
3
sinA即tanA=
3
3

∴A=30°，B=90°
∵c=3．
∴a=
3
，b=2
3
练习册系列答案
相关题目
已知数列
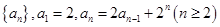
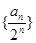⑴求证：为等差数列；
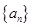⑵求的前n项和；
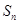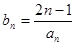⑶若，求数列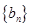中的最大值.
在△ABC中，若a=2，b=2
2
，c=
6
+
2
，则A的度数为（　　）
A．30°B．45°C．60°D．75°
在△ABC中，A=
π
3
，C=
π
6
，b=2，则此三角形的最小边长是（　　）
A．1B．2
3
-2		C．
3
-1		D．
3
2
已在△ABC中，b2-bc-2c2=0，a=
6
，cosA=
7
8
，则△ABC的面积S为______．
已知△ABC中，c-b=1，cosA=
12
13
，S△ABC=30，则a=（　　）
A．2B．4C．2
5
D．5
如图所示在△ABC中，sin2A+sin2C=sin2B+sinA．sinC
（1）求B的度数．
（2）设H为△ABC的垂心，且
BH
•
BC
=6求AC边长的最小值．
已知函数f(x)=
3
cos2x+2sinx•sin(x+
π
2
)．
（Ⅰ）求f（x）的最小正周期，最大值以及取得最大值时x的集合；
（Ⅱ）若A是锐角△ABC的内角，f（A）=0，b=5，a=7，求△ABC的面积．
如图，A、B两点都在河的对岸（不可到达），为了测量A、B两点间的距离，选取一条基线CD，A、B、C、D在一平面内．测得：CD=200m，∠ADB=∠ACB=30°，∠CBD=60°，则AB=（　　）
A．
200
3
3
m		B．200
3
m
C．100
2
m		D．数据不够，无法计算

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网