题目内容
在等比数列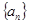 ( n∈N*)中a1>1,公比q>0,设bn=log2an,且b1+b3+b5=6,b1·b3·b5=0.
( n∈N*)中a1>1,公比q>0,设bn=log2an,且b1+b3+b5=6,b1·b3·b5=0.
(1)求证:数列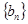 是等差数列;
是等差数列;
(2)求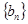 前n项和Sn及
前n项和Sn及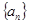 通项an.
通项an.
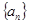 ( n∈N*)中a1>1,公比q>0,设bn=log2an,且b1+b3+b5=6,b1·b3·b5=0.
( n∈N*)中a1>1,公比q>0,设bn=log2an,且b1+b3+b5=6,b1·b3·b5=0.(1)求证:数列
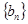 是等差数列;
是等差数列;(2)求
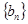 前n项和Sn及
前n项和Sn及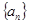 通项an.
通项an.(1)详见解析;(2)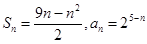
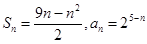
试题分析:(1)要证数列
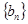 是等差数列,只须证bn+1 -bn为常数即可;(2)由等差数列的性质:下标和相等的两项和相等得到
是等差数列,只须证bn+1 -bn为常数即可;(2)由等差数列的性质:下标和相等的两项和相等得到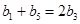 ,从而由b1+b3+b5=6得到b3=2,进而由b1·b3·b5=0可得
,从而由b1+b3+b5=6得到b3=2,进而由b1·b3·b5=0可得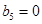 ,代入等差数列的通项公式就可求出其首项和公差,再由前n项和公式就可求出Sn并写出bn的通项公式,再由an与bn的关系就可求出an来.
,代入等差数列的通项公式就可求出其首项和公差,再由前n项和公式就可求出Sn并写出bn的通项公式,再由an与bn的关系就可求出an来.试题解析:(1)证明:
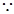 bn=
bn=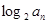 ,
, 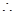 bn+1 -bn=
bn+1 -bn=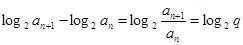 为常数,
为常数,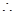 数列
数列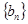 为等差数列且公差d=log2q 6分
为等差数列且公差d=log2q 6分(2)在等差数列
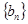 中
中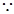 b1+b3+b5="6,"
b1+b3+b5="6," 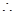 b3=2,又
b3=2,又 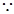 a>1,
a>1, 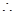 b1=log2a1>0
b1=log2a1>0 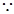 b1·b3·b5=0
b1·b3·b5=0 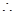 b5=0
b5=0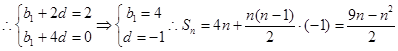 且
且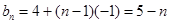
由bn=log2an得
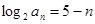
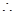 an=25-n( n∈N*) 13分
an=25-n( n∈N*) 13分
练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
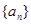 满足:
满足: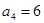 ,
,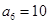 .
.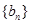 的各项均为正数,
的各项均为正数,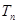 为其前
为其前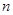 项和,若
项和,若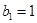 ,
,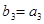 ,求
,求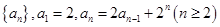
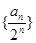 为等差数列;
为等差数列;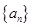 的前n项和
的前n项和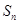 ;
;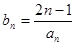 ,求数列
,求数列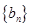 中的最大值.
中的最大值.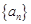 满足
满足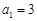 ,
,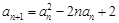 .
.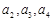 ;
;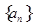 的前
的前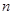 项和为
项和为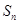 ,且
,且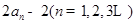 ,数列
,数列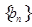 中,
中,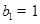 ,点
,点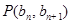 在直线
在直线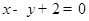 上.
上.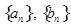 的通项
的通项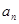 和
和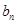 ;
;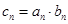 ,求数列
,求数列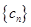 的前n项和
的前n项和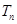 .
.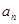 }中,
}中,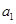 ="13" ,且前
="13" ,且前 项的算术平均数等于第
项的算术平均数等于第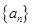 前
前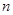 项和为
项和为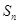 ,已知
,已知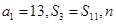 为________时,
为________时, 满足条件
满足条件 , 则
, 则 = ;
= ;