题目内容
8．将下列根式化为分数指数幂的形式．（1）$\root{3}{\sqrt{a\sqrt{a}}}$（a＞0）；
（2$\frac{1}{\root{3}{x（\root{5}{{x}^{2}}）^{2}}}$；
（3）（$\root{4}{{b}^{-\frac{2}{3}}}$）${\;}^{-\frac{2}{3}}$（b＞0）．
分析 （1）（2）（3）利用指数幂的运算性质即可得出．
解答 解：（1）原式=$（{a}^{1+\frac{1}{2}}）^{\frac{1}{6}}$=${a}^{\frac{1}{4}}$（a＞0）；
（2）原式=$\frac{1}{{x}^{（1+\frac{4}{5}）×\frac{1}{3}}}$=${x}^{-\frac{3}{5}}$；
（3）b$（{b}^{-\frac{1}{6}}）^{-\frac{2}{3}}$=${b}^{-\frac{1}{6}×（-\frac{2}{3}）}$=${b}^{\frac{1}{9}}$．（b＞0）．
点评 本题考查了指数幂的运算性质，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
16．为了得到函数$y=sin（2x-\frac{π}{3}）$的图象，只需把函数$y=cos（2x-\frac{π}{6}）$的图象（ ）
| A． | 向左平移$\frac{π}{6}$个单位长度 | B． | 向右平移$\frac{π}{6}$个单位长度 | ||
| C． | 向左平移$\frac{π}{3}$个单位长度 | D． | 向右平移$\frac{π}{3}$个单位长度 |
13．
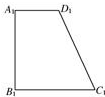如图，已知四边形ABCD的直观图是直角梯形A1B1C1D1，且A1B1=B1C1=2A1D1=4，则四边形ABCD的面积为（ ）
如图，已知四边形ABCD的直观图是直角梯形A1B1C1D1，且A1B1=B1C1=2A1D1=4，则四边形ABCD的面积为（ ）| A． | 12 | B． | 12$\sqrt{2}$ | C． | 24$\sqrt{2}$ | D． | 24 |
20．对任意x∈（0，$\frac{π}{2}$），不等式tanx•f（x）＜f′（x）恒成立，则下列不等式错误的是（ ）
| A． | f（$\frac{π}{3}$）＞$\sqrt{2}$f（$\frac{π}{4}$） | B． | f（$\frac{π}{3}$）＞2cos1•f（1） | C． | 2cos1•f（1）＞$\sqrt{2}$f（$\frac{π}{4}$） | D． | $\sqrt{2}$f（$\frac{π}{4}$）＜$\sqrt{3}$f（$\frac{π}{6}$） |