题目内容
3.已知定义在R上函数f(x)的值域是(-∞,0],并且函数f(x)单调,则方程f3(x)-3f(x)-1=0的解的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 令t=f(x),得到关于t的函数g(t),通过求导得到函数g(t)的大致图象,从而判断出所求方程解的个数.
解答 解:令t=f(x),则有t3-3t-1=0,
令g(t)=t3-3t-1,g′(t)=3t2-3=3(t+1)(t-1),
于是可得:g(t)的图象如下: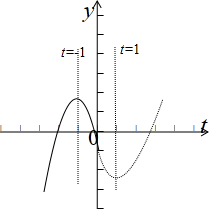 ,
,
∴方程t3-3t-1=0有3个不同的解,其中2个解是负的,
而函数f(x)的值域是(-∞,0],并且函数f(x)单调,
∴方程f3(x)-3f(x)-1=0有2个不同的实数解,
故选:B.
点评 本题考查了函数的单调性问题,考查导数的应用,数形结合思想,是一道中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.不等式ax2+4x+a<1+x2对一切x∈R恒成立,则实数a的取值范围是( )
| A. | (3,+∞) | B. | (-∞,-1) | C. | (-∞,1) | D. | (-∞,-1)∪(3,+∞) |
18.某班一次数学考试后的成绩如表所示:
据此估计,该班本次数学测试的平均成绩为82.
| 成绩分组 | [60,70) | [70,80) | [80,90) | [90,100) |
| 人数 | 5 | 15 | 20 | 10 |
12.方程1-|x|=$\sqrt{1-{y}^{2}}$表示的曲线是( )
| A. | 一个圆 | B. | 两个圆 | C. | 半个圆 | D. | 两个半圆 |
13.方程2x+x=0的解的个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |