题目内容
13．
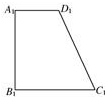如图，已知四边形ABCD的直观图是直角梯形A1B1C1D1，且A1B1=B1C1=2A1D1=4，则四边形ABCD的面积为（ ）| A． | 12 | B． | 12$\sqrt{2}$ | C． | 24$\sqrt{2}$ | D． | 24 |
分析 如图，取∠GB1C1=135°，确定平面图形的形状，求出底边边长，上底边边长，以及高，然后求出面积．
解答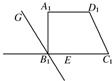 
解：如图，取∠GB1C1=135°，过点A1作A1E∥GB1，
易求得B1E=4，A1E=4$\sqrt{2}$，故以B1C1和B1A1为坐标轴建立直角坐标系，由直观图原则，B，C与B1，C1重合，然后过点E作B1A1的平行线，且使得AE=2A1E=8$\sqrt{2}$，
即得点A，然后过A作AD∥BC且使得AD=2，
即四边形ABCD上底和下底边长分别为2，4，高为8$\sqrt{2}$，
故其面积S=$\frac{1}{2}$（2+4）×8$\sqrt{2}$=24$\sqrt{2}$．
故选：C．
点评 本题考查平面图形的直观图，考查计算能力，作图能力，是基础题．
练习册系列答案
心算口算巧算一课一练系列答案
应用题作业本系列答案
相关题目
3．下列函数中，在（0，+∞）上为增函数的是（ ）
| A． | y=$\sqrt{x+1}$ | B． | y=（x-2）2 | C． | y=3-x | D． | y=log0.1（x+1） |
4．下列各式中，值为$\frac{{\sqrt{3}}}{2}$的是（ ）
| A． | $\sqrt{\frac{{1+cos{{120}°}}}{2}}$ | B． | ${cos^2}\frac{π}{12}-{sin^2}\frac{π}{12}$ | ||
| C． | cos42°sin12°-sin42°cos12° | D． | $\frac{{tan{{15}°}}}{{1-{{tan}^2}{{15}°}}}$ |