题目内容
【题目】已知自然数![]() 有20个正整数因子(包括1和本身),它们从小到大依次记作
有20个正整数因子(包括1和本身),它们从小到大依次记作![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,且序号为
,且序号为![]() 的因数为
的因数为![]() .求自然数
.求自然数![]() .
.
【答案】2000
【解析】
因为![]() 是
是![]() 的因数,
的因数,
所以,![]() 与
与![]() 是
是![]() 的因数.
的因数.
于是,![]() ,
,![]() .
.
∴![]() .
.![]()
∵![]() ,
,
∴![]() .
.
∴![]() .此时,
.此时,![]() ,
,![]() .
.
由![]() 知,
知,![]() 含有1,2,4,5,10,20这六个正整数因子,
含有1,2,4,5,10,20这六个正整数因子,
所以![]() 至少含有2和5这两个质因子.
至少含有2和5这两个质因子.
又![]() 有20个正因子,
有20个正因子,![]() ,
,
故![]() 可设为
可设为![]() (
(![]() 为不等于2和5的质数)、
为不等于2和5的质数)、![]() 、
、![]() 或
或![]() .
.
(1)当![]() 时,
时,
①当![]() 时,
时,![]() ,
,![]() ,…,
,…,![]() 依次为1,2,3,4,5,6,8,10.此时,
依次为1,2,3,4,5,6,8,10.此时,![]() ,与
,与![]() 相矛盾.
相矛盾.
②当![]() 时,
时,![]() ,
,![]() ,…,
,…,![]() 依次为1,2,4,5,7,8,10,14.此时,
依次为1,2,4,5,7,8,10,14.此时,![]() ,与
,与![]() 相矛盾.
相矛盾.
③当![]() 时,
时,![]() ,
,![]() ,
,![]() ,…,
,…,![]() 依次为1,2,4,5,8,10,
依次为1,2,4,5,8,10,![]() ,16或为1,2,4,5,8,10,16,
,16或为1,2,4,5,8,10,16,![]() ,与
,与![]() 相矛盾.
相矛盾.
④当![]() 时,
时,![]() 的正因数为1,2,4,5,8,10,16,20,40,80,
的正因数为1,2,4,5,8,10,16,20,40,80,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,….
,….
∴![]() ,
,![]() ,
,![]() ,
,![]() .
.
∴![]() .
.
于是,![]() ,不为质数,
,不为质数,
故![]() .
.
(2)当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,![]() .不满足
.不满足![]() .
.
(3)当![]() 时,
时,![]() ,与
,与![]() 相矛盾.
相矛盾.
(4)当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .显然满足
.显然满足![]() ,
,![]() .
.
∴![]() .
.
故所求的自然数![]() 为2000.
为2000.

【题目】为了提高学生的身体素质,某校高一、高二两个年级共![]() 名学生同时参与了“我运动,我健康,我快乐”的跳绳、踢毽等系列体育健身活动.为了了解学生的运动状况,采用分层抽样的方法从高一、高二两个年级的学生中分别抽取
名学生同时参与了“我运动,我健康,我快乐”的跳绳、踢毽等系列体育健身活动.为了了解学生的运动状况,采用分层抽样的方法从高一、高二两个年级的学生中分别抽取![]() 名和
名和![]() 名学生进行测试.下表是高二年级的
名学生进行测试.下表是高二年级的![]() 名学生的测试数据(单位:个/分钟):
名学生的测试数据(单位:个/分钟):
学生编号 | 1 | 2 | 3 | 4 | 5 |
跳绳个数 | 179 | 181 | 168 | 177 | 183 |
踢毽个数 | 85 | 78 | 79 | 72 | 80 |
(1)求高一、高二两个年级各有多少人?
(2)设某学生跳绳![]() 个/分钟,踢毽
个/分钟,踢毽![]() 个/分钟.当
个/分钟.当![]() ,且
,且![]() 时,称该学生为“运动达人”.
时,称该学生为“运动达人”.
①从高二年级的学生中任选一人,试估计该学生为“运动达人”的概率;
②从高二年级抽出的上述![]() 名学生中,随机抽取
名学生中,随机抽取![]() 人,求抽取的
人,求抽取的![]() 名学生中为“span>运动达人”的人数
名学生中为“span>运动达人”的人数![]() 的分布列和数学期望.
的分布列和数学期望.
【题目】为抑制房价过快上涨和过度炒作,各地政府响应中央号召,因地制宜出台了系列房价调控政策.某市为拟定出台“房产限购的年龄政策”![]() 为了解人们对“房产限购年龄政策”的态度,对年龄在
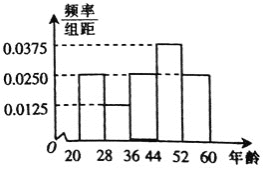
为了解人们对“房产限购年龄政策”的态度,对年龄在![]() 岁的人群中随机调查100人,调查数据的频率分布直方图和支持“房产限购”的人数与年龄的统计结果如下:
岁的人群中随机调查100人,调查数据的频率分布直方图和支持“房产限购”的人数与年龄的统计结果如下:
年龄 |
|
|
|
|
|
支持的人数 | 15 | 5 | 15 | 28 | 17 |
(1)由以上统计数据填![]() 列联表,并判断能否在犯错误的概率不超过
列联表,并判断能否在犯错误的概率不超过![]() 的前提下认为以44岁为分界点的不同人群对“房产限购年龄政策”的支持度有差异;
的前提下认为以44岁为分界点的不同人群对“房产限购年龄政策”的支持度有差异;
44岁以下 | 44岁及44岁以上 | 总计 | |
支持 | |||
不支持 | |||
总计 |
(2)若以44岁为分界点,从不支持“房产限购”的人中按分层抽样的方法抽取8人参加政策听证会.现从这8人中随机抽2人.
①抽到1人是44岁以下时,求抽到的另一人是44岁以上的概率.
②记抽到44岁以上的人数为X,求随机变量X的分布列及数学期望.
参考数据:
|
|
|
|
|
|
|
|
|
|
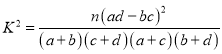 ,其中
,其中![]() .
.