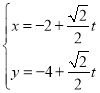题目内容
【题目】空间中有不共面的![]() 个点
个点![]() .求证:存在无穷个平面,恰好通过其中的两个点.
.求证:存在无穷个平面,恰好通过其中的两个点.
【答案】见解析
【解析】
由于![]() 个点不共面,故也不共线.下面证明,必存在一条直线恰好通过其中的两个点.
个点不共面,故也不共线.下面证明,必存在一条直线恰好通过其中的两个点.
![]() 个点作两两连线,最多有
个点作两两连线,最多有![]() 条,每条线外的点到直线的非零距离中,必有最小的,设
条,每条线外的点到直线的非零距离中,必有最小的,设![]() 点到直线
点到直线![]() 的距离
的距离![]() 为最短(如图).
为最短(如图).
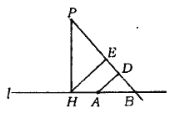
我们来证明,![]() 恰好通过两个已知点.
恰好通过两个已知点.
若不然,直线![]() 上至少有3个已知点,其中必有两点在
上至少有3个已知点,其中必有两点在![]() 的同侧.
的同侧.
记![]() 、
、![]() 在
在![]() 的同侧,有
的同侧,有![]() .
.
连结![]() ,作
,作![]() 于
于![]() ,
,![]() 于
于![]() .则
.则![]() ,
,
即存在点![]() 到直线
到直线![]() 的距离小于
的距离小于![]() .这与
.这与![]() 的最小性矛盾.故
的最小性矛盾.故![]() 恰好通过两个已知点.
恰好通过两个已知点.
此时,![]() 之外还有
之外还有![]() 个点,每个点与
个点,每个点与![]() 可以确定一个平面,最多可以确定
可以确定一个平面,最多可以确定![]() 个平面,但通过
个平面,但通过![]() 可以作无穷个平面,故去掉那
可以作无穷个平面,故去掉那![]() 个平面后,还有无穷个通过
个平面后,还有无穷个通过![]() ,它们中的每一个都恰好通过两个已知点.
,它们中的每一个都恰好通过两个已知点.

练习册系列答案
相关题目