题目内容
(本小题满分12分)
(1)已知函数f(x)=2x-x2,问方程f(x)=0在区间[-1,0]内是否有解,为什么?
(2)若方程ax2-x-1=0在(0,1)内恰有一解,求实数a的取值范围.
(1)已知函数f(x)=2x-x2,问方程f(x)=0在区间[-1,0]内是否有解,为什么?
(2)若方程ax2-x-1=0在(0,1)内恰有一解,求实数a的取值范围.
(1) 方程f(x)=0在区间[-1,0]内有解.(2) (2,+∞).
试题分析:
(1)因为第一问中,f(-1)=2-1-(-1)2=-
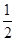 <0,
<0,f(0)=20-02=1>0,结合零点存在性定理可知,结论。
(2)方程ax2-x-1=0在(0,1)内恰有一解,即函数f(x)=ax2-x-1在(0,1)内恰有一个零点,则只要满足端点的函数值一号即可。
(1) 因为f(-1)=2-1-(-1)2=-
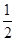 <0,
<0,f(0)=20-02=1>0,
而函数f(x)=2x-x2的图象是连续曲线,所以f(x)在区间[-1,0]内有零点,即方程f(x)=0在区间[-1,0]内有解.
(2)∵方程ax2-x-1=0在(0,1)内恰有一解,即函数f(x)=ax2-x-1在(0,1)内恰有一个零点,
∴f(0)·f(1)<0,即-1×(a-2)<0,解得a>2.
故a的取值范围为(2,+∞).
点评:解决该试题的关键是根据零点的概念将方程解的问题转换为关于图像与图像的交点问题来处理得到结论。

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
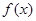 对任意的实数
对任意的实数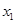 ,
,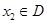 ,均有
,均有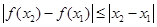 ,则称函数
,则称函数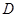 上的“平缓函数”.
上的“平缓函数”. 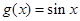 和
和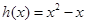 是不是实数集R上的“平缓函数”,并说明理由;
是不是实数集R上的“平缓函数”,并说明理由; 对所有的正整数
对所有的正整数 都有
都有 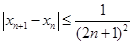 ,设
,设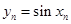 ,
, 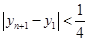 .
.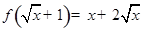 ,则
,则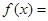 。(指出
。(指出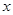 范围)
范围)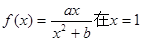 处取得极值2。
处取得极值2。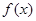 的解析式;
的解析式; 为增函数;
为增函数; ”:
”: ,
, ,则函数
,则函数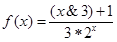
 在区间
在区间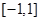 上是增函数,实数a组成几何A,设关于x的方程
上是增函数,实数a组成几何A,设关于x的方程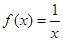 的两个非零实根
的两个非零实根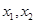 ,实数m使得不等式
,实数m使得不等式 使得对任意
使得对任意 及
及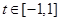 恒成立,则m的解集是( )
恒成立,则m的解集是( )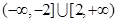
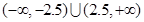


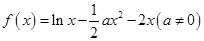 存在单调递减区间,则实数
存在单调递减区间,则实数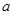 的取值
的取值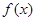 对于其定义域内的某一数
对于其定义域内的某一数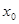 ,有
,有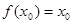 ,则称
,则称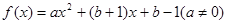 .
.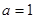 ,
, 时,求函数
时,求函数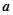 的取值范围;
的取值范围;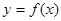 图象上两个点A、B的横坐标是函数
图象上两个点A、B的横坐标是函数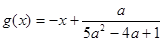 的图象上,求实数b的最小值.
的图象上,求实数b的最小值.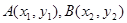 ,则线段AB的中点坐标为
,则线段AB的中点坐标为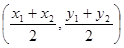 )
)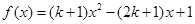 ,
, .
.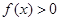 恒成立,求实数
恒成立,求实数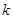 的取值范围;
的取值范围;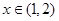 时,
时,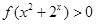 恒成立,求实数
恒成立,求实数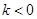 时,解不等式
时,解不等式