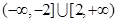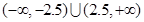题目内容
已知函数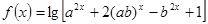
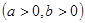 ,求使
,求使 成立的
成立的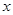 的取值范围。(10分)
的取值范围。(10分)
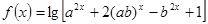
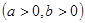 ,求使
,求使 成立的
成立的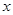 的取值范围。(10分)
的取值范围。(10分)当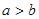 时,
时,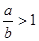 ,
, ,当
,当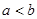 时,
时,
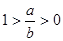 ,
,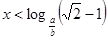 ,当
,当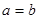 时 ,
时 ,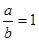 ,
,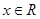
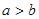 时,
时,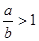 ,
, ,当
,当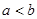 时,
时,
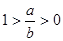 ,
,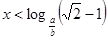 ,当
,当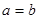 时 ,
时 ,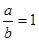 ,
,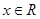
试题分析:由已知
 ,即
,即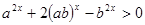 , ……2分
, ……2分两边都除以
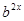 得,
得,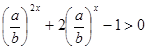 .
.设
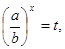 则
则 ,不等式可化为
,不等式可化为 ,
, ,即
,即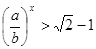 . ……7分
. ……7分当
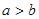 时,
时,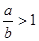 ,
, , ……8分
, ……8分当
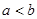 时,
时,
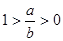 ,
,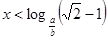 , ……9分
, ……9分当
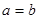 时 ,
时 ,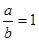 ,
,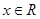 . ……10分
. ……10分点评:函数的性质及其应用历来是考查的重点,要把各种函数的性质联系起来,综合灵活应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
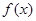 对任意的实数
对任意的实数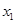 ,
,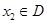 ,均有
,均有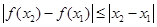 ,则称函数
,则称函数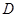 上的“平缓函数”.
上的“平缓函数”. 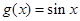 和
和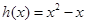 是不是实数集R上的“平缓函数”,并说明理由;
是不是实数集R上的“平缓函数”,并说明理由;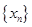 对所有的正整数
对所有的正整数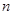 都有
都有 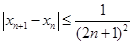 ,设
,设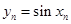 ,
, 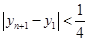 .
.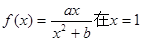 处取得极值2。
处取得极值2。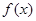 的解析式;
的解析式; 为增函数;
为增函数;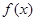
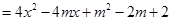 的图像与
的图像与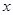 轴有两个交点
轴有两个交点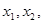 试判断函数
试判断函数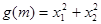 有没有最大值或最小值,并说明理由.
有没有最大值或最小值,并说明理由. 在区间
在区间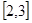 上都是减函数,求实数
上都是减函数,求实数 的取值范围.
的取值范围.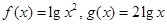

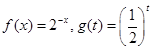
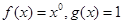
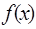 为奇函数,且在
为奇函数,且在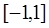 上为增函数,
上为增函数,  , 若
, 若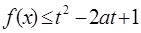 对所有
对所有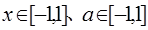 都成立,求
都成立,求 的取值范围。
的取值范围。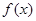 是定义在
是定义在 上的单调增函数,满足
上的单调增函数,满足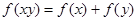 ,
,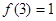 ,
,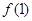 ;
;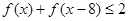 ,求
,求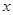 的取值范围。
的取值范围。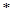 ”:
”: ,
, ,则函数
,则函数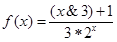
 在区间
在区间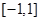 上是增函数,实数a组成几何A,设关于x的方程
上是增函数,实数a组成几何A,设关于x的方程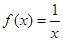 的两个非零实根
的两个非零实根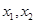 ,实数m使得不等式
,实数m使得不等式 使得对任意
使得对任意 及
及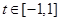 恒成立,则m的解集是( )
恒成立,则m的解集是( )