题目内容
【题目】已知函数f(x)=x2![]() ax3(a>0),x∈R.若对任意的x1∈(2,+∞),都存在x2∈(1,+∞),使得f(x1)
ax3(a>0),x∈R.若对任意的x1∈(2,+∞),都存在x2∈(1,+∞),使得f(x1)![]() f(x2)=1,则a的取值范围是_____.
f(x2)=1,则a的取值范围是_____.
【答案】![]()
【解析】
由![]() =﹣2ax2+2x
=﹣2ax2+2x![]() ,令
,令![]() =0,得
=0,得![]() ,根据对任意的x1∈(2,+∞),都存在x2∈(1,+∞),使得f(x1)
,根据对任意的x1∈(2,+∞),都存在x2∈(1,+∞),使得f(x1)![]() f(x2)=1,分
f(x2)=1,分![]() ,
, ![]() ,
,
![]() 三种情况讨论f(x1),f(x2)的值域即可.
三种情况讨论f(x1),f(x2)的值域即可.
因为![]() =﹣2ax2+2x
=﹣2ax2+2x![]() ,
,
令![]() =0得
=0得![]() ,
,
①:当![]() ,即a≥1时,
,即a≥1时,![]() <0,在x∈[1,+∞)恒成立,所以f(x)在[1,+∞)递减,
<0,在x∈[1,+∞)恒成立,所以f(x)在[1,+∞)递减,
∵![]() ,
,![]() ,
,
若对任意的x1∈(2,+∞),都存在x2∈(1,+∞),使得f(x1)![]() f(x2)=1,
f(x2)=1,
所以f(x1)的值域为(![]() ),f(x2)的值域为(
),f(x2)的值域为(![]() ),
),
由f(x1)![]() f(x2)=1得:
f(x2)=1得:![]() .
.
显然,当f(x1)→﹣∞时,![]() →0(负数),故要满足结论,首先需满足:
→0(负数),故要满足结论,首先需满足:
![]() ,
,![]() ,解得
,解得![]() .
.
所以![]() .
.
②当![]() ,即
,即![]() 时,f(x1)在(2,+∞)上递减,故此时f(x1)
时,f(x1)在(2,+∞)上递减,故此时f(x1)![]() ,
,
f(x2)在(1,![]() )递增,在
)递增,在![]() 递减,故
递减,故![]() 0.
0.
此时只需![]() 即可,解得
即可,解得![]() .
.
③当![]() ,即
,即![]() 时,f(x1),f(x2)的最大值都是
时,f(x1),f(x2)的最大值都是![]() 0,所以
0,所以![]() 能取到所有正实数,
能取到所有正实数,
而![]() ,故此时不满足题意.
,故此时不满足题意.
综上,a的取值范围是[![]() ].
].
故答案为:![]()

 名校课堂系列答案
名校课堂系列答案【题目】已知对某校的100名学生进行不记名问卷调查,内容为一周的课外阅读时长和性别等进行统计,如表:
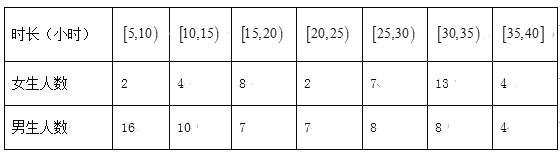
(1)课外阅读时长在20以下的女生按分层抽样的方式随机抽取7人,再从7人中随机抽取2人,求这2人课外阅读时长不低于15的概率;
(2)将课外阅读时长为25以上的学生视为“阅读爱好”者,25以下的学生视为“非阅读爱好”者,根据以上数据完成2×2列联表:
非阅读爱好者 | 阅读爱好者 | 总计 | |
女生 | |||
男生 | |||
总计 |
能否在犯错概率不超过0.01的前提下,认为学生的“阅读爱好”与性别有关系?
附:![]() ,
,
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
【题目】体育测试成绩分为四个等级:优、良、中、不及格.某班50名学生参加测试结果如下:
等级 | 优(86~100分) | 良(75~85分) | 中(60~74分) | 不及格(1~59分) |
人数 | 5 | 21 | 22 | 2 |
(1)估计该班学生体育测试的平均成绩;
(2)从该班任意抽取1名学生,求这名学生的测试成绩为“优”或“良”的概率.