题目内容
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).M是曲线
为参数).M是曲线![]() 上的动点,将线段OM绕O点顺时针旋转
上的动点,将线段OM绕O点顺时针旋转![]() 得到线段ON,设点N的轨迹为曲线
得到线段ON,设点N的轨迹为曲线![]() .以坐标原点O为极点,
.以坐标原点O为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)在(1)的条件下,若射线![]() 与曲线
与曲线![]() 分别交于A, B两点(除极点外),且有定点
分别交于A, B两点(除极点外),且有定点![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)![]() ,
,![]() ; (2)
; (2)![]() .
.
【解析】
(1)将曲线C1的参数方程转化为普通方程,然后由普通方程转化为极坐标方程;再用N表示出M,根据点M在曲线C1上,采用相关点法,求轨迹C2的极坐标方程;
(2)根据已知条件,求得![]() ,通过
,通过![]() 求解.
求解.
(1)由题设,得![]() 的直角坐标方程为
的直角坐标方程为![]() ,即
,即![]() ,
,
故![]() 的极坐标方程为
的极坐标方程为![]() ,即
,即![]() .
.
设点![]() ,则由已知得
,则由已知得![]() ,代入
,代入![]() 的极坐标方程得
的极坐标方程得![]() ,
,
即![]() .
.
(2)将![]() 代入
代入![]() 的极坐标方程得
的极坐标方程得![]() ,
,
又因为![]() ,所以
,所以![]() ,
,
![]() ,
,
所以![]() .
.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
【题目】在测量一根新弹簧的劲度系数时,测得了如下的结果:
所挂重量( | 1 | 2 | 3 | 5 | 7 | 9 |
弹簧长度( | 11 | 12 | 12 | 13 | 14 | 16 |
(1)请在下图坐标系中画出上表所给数据的散点图;

(2)若弹簧长度与所挂物体重量之间的关系具有线性相关性,请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ;
;
(3)根据回归方程,求挂重量为![]() 的物体时弹簧的长度.所求得的长度是弹簧的实际长度吗?为什么?
的物体时弹簧的长度.所求得的长度是弹簧的实际长度吗?为什么?
注:本题中的计算结果保留小数点后两位.
(参考公式: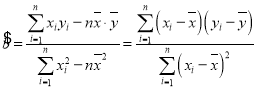 ,
,![]() )
)
(参考数据:![]() ,
,![]() )
)


