Question

【题目】如图，某学校拟建一块五边形区域的“读书角”，三角形区域ABE为书籍摆放区，沿着AB、AE处摆放折线形书架（书架宽度不计），四边形区域为BCDE为阅读区，若∠BAE＝60°，∠BCD＝∠CDE＝120°，DE＝3BC＝3CD＝m．

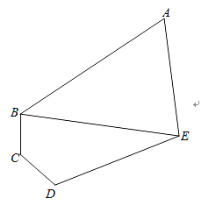
（1）求两区域边界BE的长度；

（2）若区域ABE为锐角三角形，求书架总长度AB+AE的取值范围．

Answer 1

【答案】（1）（2）

【解析】

（1）连接BD，由余弦定理可得BD，由已知可求∠CDB＝∠CBD＝30°，∠CDE＝120°，可得∠BDE＝90°，利用勾股定理即可得解BE的值；（2）设∠ABE＝α，由正弦定理，可得AB＝4sin（120°﹣α），AE＝4sinα，利用三角函数恒等变换的应用化简可得AB+AE＝12sin（α+30°），结合范围60°＜α+30°＜120°，利用正弦函数的性质可求AB+AE的最大值，从而得解．

⑴连接BD，在△BDC中，，∠BCD=120°，

由余弦定理,

得，得

又BC=CD，∠BCD=120°，

，.

△ABE中，BD=3，，由勾股定理.

故.

⑵设，

则,

在△ABE中，

由正弦定理.

，，

故

=

，

△ABE为锐角三角形，

故，，

，

所以暑假的总长度AB+AE的取值范围是，