��Ŀ����
����Ŀ����֪��ijУ��100��ѧ�����в������ʾ����飬����Ϊһ�ܵĿ����Ķ�ʱ�����Ա�Ƚ���ͳ�ƣ������
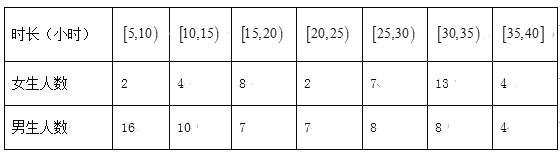
��1�������Ķ�ʱ����20���µ�Ů�����ֲ�����ķ�ʽ�����ȡ7�ˣ��ٴ�7���������ȡ2�ˣ�����2�˿����Ķ�ʱ��������15�ĸ��ʣ�
��2���������Ķ�ʱ��Ϊ25���ϵ�ѧ����Ϊ���Ķ����á��ߣ�25���µ�ѧ����Ϊ�����Ķ����á��ߣ����������������2��2��������
���Ķ������� | �Ķ������� | �ܼ� | |
�� | |||
���� | |||
�ܼ� |
�ܷ��ڷ������ʲ�����0.01��ǰ���£���Ϊѧ���ġ��Ķ����á����Ա��й�ϵ��
����![]() ��
��
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
���𰸡���1��![]() ����2������������������.
����2������������������.
��������
��1�������Ķ�ʱ����20���µ�Ů������2+4+8=14�ˣ����ֲ�����ķ�ʽ�����ȡ7�ˣ�ʱ����![]() ��
��![]() ��Ů���ֱ���1�ˣ���Ϊa����2�ˣ���Ϊ
��Ů���ֱ���1�ˣ���Ϊa����2�ˣ���Ϊ![]() ����4�ˣ���Ϊ
����4�ˣ���Ϊ![]() �����г������¼��ռ䣬���ҳ���2�˿����Ķ�ʱ��������15���¼������ɣ�2��Ů������16���Ƿ��Ķ������ߣ�24�����Ķ������ߣ���������40���Ƿ��Ķ������ߣ�20�����Ķ������ߣ����������������
�����г������¼��ռ䣬���ҳ���2�˿����Ķ�ʱ��������15���¼������ɣ�2��Ů������16���Ƿ��Ķ������ߣ�24�����Ķ������ߣ���������40���Ƿ��Ķ������ߣ�20�����Ķ������ߣ����������������![]() ��ֵ���ö����м�����ٽ�ֵ�жϼ���.
��ֵ���ö����м�����ٽ�ֵ�жϼ���.
�⣺��1�������Ķ�ʱ����20���µ�Ů������2+4+8=14�ˣ����ֲ�����ķ�ʽ�����ȡ7�ˣ�ʱ����![]() ��
��![]() ��Ů���ֱ���1�ˣ���Ϊa����2�ˣ���Ϊ
��Ů���ֱ���1�ˣ���Ϊa����2�ˣ���Ϊ![]() ����4�ˣ���Ϊ
����4�ˣ���Ϊ![]() ����
����
��7���������ȡ2�˰����Ļ����¼�Ϊ��![]()
��21����
��2�˿����Ķ�ʱ��������15���������¼��У�![]() ��6����
��6����
��2�˿����Ķ�ʱ��������15�ĸ���![]()
��2��
���Ķ������� | �Ķ������� | �ܼ� | |
�� | 16 | 24 | 40 |
���� | 40 | 20 | 60 |
�ܼ� | 56 | 44 | 100 |
��![]()
�ڷ������ʲ�����0.01��ǰ���£���Ϊѧ�������Ķ����������Ա��й�ϵ.

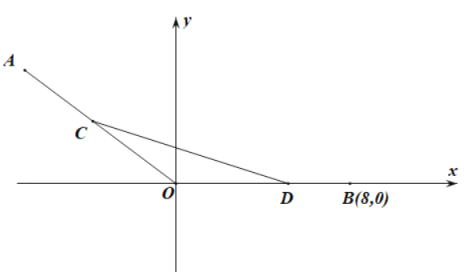
����Ŀ��ijͬѧ������㷨��������![]() ��ijһ�������ڵ�ͼ��ʱ���г�������������˲�������:
��ijһ�������ڵ�ͼ��ʱ���г�������������˲�������:
| 0 |
| �� |
|
|
x |
|
| |||
| 0 | 2 | 0 | 0 |
��1��������ϱ����ݣ�д������![]() �Ľ���ʽ����ֱ��д��������ɣ�
�Ľ���ʽ����ֱ��д��������ɣ�
��2������![]() �ĵ����������䣻
�ĵ����������䣻
��3����![]() ����֪����
����֪����![]() ������
������![]() �ϵ����ֵ��img src="http://thumb.zyjl.cn/questionBank/Upload/2020/11/26/20/139c9676/SYS202011262014544768390673_ST/SYS202011262014544768390673_ST.013.png" width="24" height="24" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />����t��ֵ�Լ�����
�ϵ����ֵ��img src="http://thumb.zyjl.cn/questionBank/Upload/2020/11/26/20/139c9676/SYS202011262014544768390673_ST/SYS202011262014544768390673_ST.013.png" width="24" height="24" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />����t��ֵ�Լ�����![]() ������[
������[![]() �ϵ���Сֵ.
�ϵ���Сֵ.