题目内容
【题目】前段时间,某机构调查人们对屯商平台“618”活动的认可度(分为:强烈和一般两类),随机抽取了100人统计得到2×2列联表的部分数据如表:
一般 | 强烈 | 合计 | |
男 | 45 | ||
女 | 10 | ||
合计 | 75 | 100 |
(1)补全2×2列联表中的数据;
(2)判断能否有95%的把握认为人们的认可度是否为“强烈”与性别有关?
参考公式及数据: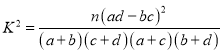
| 0.05 | 0.025 | 0.010 | 0.005 |
| 3.841 | 5.024 | 6.635 | 7.879 |
【答案】(1)列联表见解析;(2)没有
【解析】
(1)通过题意,分别求出认可度一般的男、女人数,认可度强烈的男、女人数,填写列联表;
(2)根据列联表,计算出![]() 的值,然后进行判断,得到结论.
的值,然后进行判断,得到结论.
(1)因为总人数![]() 人,认可度一般有
人,认可度一般有![]() 人,所以认可度强烈有
人,所以认可度强烈有![]() 人,
人,
因为认可度强烈中,女有![]() 人,所以男有
人,所以男有![]() 人,
人,
因为男共有![]() 人,所以认可度一般男有
人,所以认可度一般男有![]() 人,女有
人,女有![]() 人,
人,
填写列联表如下;
一般 | 强烈 | 合计 | |
男 | 30 | 15 | 45 |
女 | 45 | 10 | 55 |
合计 | 75 | 25 | 100 |
(2)根据表中数据,
计算![]() ,
,
所以没有![]() 的把握认为人们的认可度是否为“强烈”与性别有关.
的把握认为人们的认可度是否为“强烈”与性别有关.

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案【题目】某地随着经济的发展,居民收入逐年增长该地一建设银行统计连续五年的储蓄存款(年底余额)得到下表:
年份x | 2014 | 2015 | 2016 | 2017 | 2018 |
储蓄存款y(千亿元) | 5 | 6 | 7 | 8 | 10 |
为便于计算,工作人员将上表的数据进行了处理(令![]()
![]() ),得到下表:
),得到下表:
时间t | 1 | 2 | 3 | 4 | 5 |
储蓄存款z | 0 | 1 | 2 | 3 | 5 |
(1)求z关于t的线性回归方程;
(2)通过(1)中的方程,求出y关于x的回归方程;
(3)用所求回归方程预测到2020年年底,该地储蓄存款额可达多少?
附:线性回归方程![]() ,其中
,其中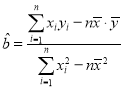 ,
,![]() .
.
【题目】某运动员射击一次所得环数![]() 的分布列如下:
的分布列如下:
| 8 | 9 | 10 |
| 0.4 | 0.4 | 0.2 |
现进行两次射击,且两次射击互不影响,以该运动员两次射击中最高环数作为他的成绩,记为![]() .
.
(1)求该运动员两次命中的环数相同的概率;
(2)求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.