题目内容
【题目】在直角坐标系中,已知椭圆![]() 经过点
经过点![]() ,且其左右焦点的坐标分别是
,且其左右焦点的坐标分别是![]() ,
,![]() .
.
(1)求椭圆![]() 的离心率及标准方程;
的离心率及标准方程;
(2)设![]() 为动点,其中
为动点,其中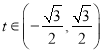 ,直线
,直线![]() 经过点
经过点![]() 且与椭圆
且与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,若
两点,若![]() 为
为![]() 的中点,是否存在定点
的中点,是否存在定点![]() ,使
,使![]() 恒成立?若存在,求点
恒成立?若存在,求点![]() 的坐标;若不存在,说明理由
的坐标;若不存在,说明理由
【答案】(1)![]() ,
,![]() ;(2)在定点
;(2)在定点![]()
【解析】
(1)根据椭圆的焦点得到![]() ,根据椭圆过
,根据椭圆过![]() 点,由椭圆的定义得到
点,由椭圆的定义得到![]() ,再求出
,再求出![]() ,从而得到椭圆的离心率和标准方程;
,从而得到椭圆的离心率和标准方程;
(2)设![]() ,
,![]() ,则
,则![]() ,
,![]() ,利用点差法,得到
,利用点差法,得到![]() ,从而表示出线段
,从而表示出线段![]() 的垂直平分线,再根据直线过定点,得到关于
的垂直平分线,再根据直线过定点,得到关于![]() 的方程组,得到定点
的方程组,得到定点![]() 的坐标.
的坐标.
(1)设椭圆![]() 方程:
方程:![]() .
.
∴![]() .
.
∵椭圆![]() 经过点
经过点![]() ,
,
∴![]() ,
,
∴![]() ,可得
,可得![]() .
.
椭圆![]() 的离心率为
的离心率为![]() ,椭圆标准方程:
,椭圆标准方程:![]() .
.
(2)设![]() ,
,![]() ,
,
因为![]() 为
为![]() 中点,
中点,
则![]() ,
,![]() .
.
∵![]() 、
、![]() 在曲线
在曲线![]() 上,∴
上,∴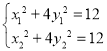 ,
,
将以上两式相减得:![]() .
.
所以得到![]() ,
,
∴线段![]() 的垂直平分线方程:
的垂直平分线方程:![]()
![]()
![]() ,
,
整理得![]()
令![]() ,得
,得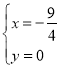
故线段![]() 的垂直平分线过定点
的垂直平分线过定点![]() .
.
所以存在定点![]() ,使
,使![]() 恒成立.
恒成立.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】如图,已知抛物线![]() 的焦点为
的焦点为![]() ,椭圆
,椭圆![]() 的中心在原点,
的中心在原点,![]() 为其右焦点,点
为其右焦点,点![]() 为曲线
为曲线![]() 和
和![]() 在第一象限的交点,且
在第一象限的交点,且![]() .
.

(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设![]() 为抛物线
为抛物线![]() 上的两个动点,且使得线段
上的两个动点,且使得线段![]() 的中点
的中点![]() 在直线
在直线![]() 上,
上,
![]() 为定点,求
为定点,求![]() 面积的最大值.
面积的最大值.
【题目】前段时间,某机构调查人们对屯商平台“618”活动的认可度(分为:强烈和一般两类),随机抽取了100人统计得到2×2列联表的部分数据如表:
一般 | 强烈 | 合计 | |
男 | 45 | ||
女 | 10 | ||
合计 | 75 | 100 |
(1)补全2×2列联表中的数据;
(2)判断能否有95%的把握认为人们的认可度是否为“强烈”与性别有关?
参考公式及数据: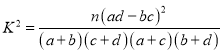
| 0.05 | 0.025 | 0.010 | 0.005 |
| 3.841 | 5.024 | 6.635 | 7.879 |